Y x 2 y =4 (1) ie, a circle of radius 2 cen tered at the origin W e start b y asso ciating p osition v ector r to eac h p oin t(x;Only equations 1, 3, 5 and 6 are centerradius forms The second equation graphs a straight line;This video explains how to derive the area formula for a circle using integrationhttp//mathispower4ucom

Find A Parameterization For The Circle X 2 2 Y 2 1 Starting At The Point 1 0 And Moving Clockwise Twice Around The Circle Using The Central Angle 0 In The Figure Below
X2 y2 1 circle
X2 y2 1 circle-Find the volume under the paraboloid z = 4(x2) 2y 2 over the region bounded by the circles (x1) 2 y 2 = 1 and (x2) 2 y 2 = 4 Solution At first glance, this seems like a very hard volume to compute as the region R (shown in Figure 1433 (a)) has a hole in it, cutting out a strange portion of the surface, as shown in part (b) of the Expand the equation of the circle #x^2 2x 1 y^2 2y 1 = 25# #x^2 y^2 2x 2y 2 = 25# Differentiate both sides with respect to x using implicit differentiation and the power rule #d/dx(x^2 y^2 2x 2y 2) = d/dx(25)# #2x 2y(dy/dx) 2 2(dy/dx) = 0# #2y(dy/dx) 2(dy/dx) = 2 2x# #dy/dx(2y 2) = 2 2x# #dy/dx = (2 2x)/(2y 2)#
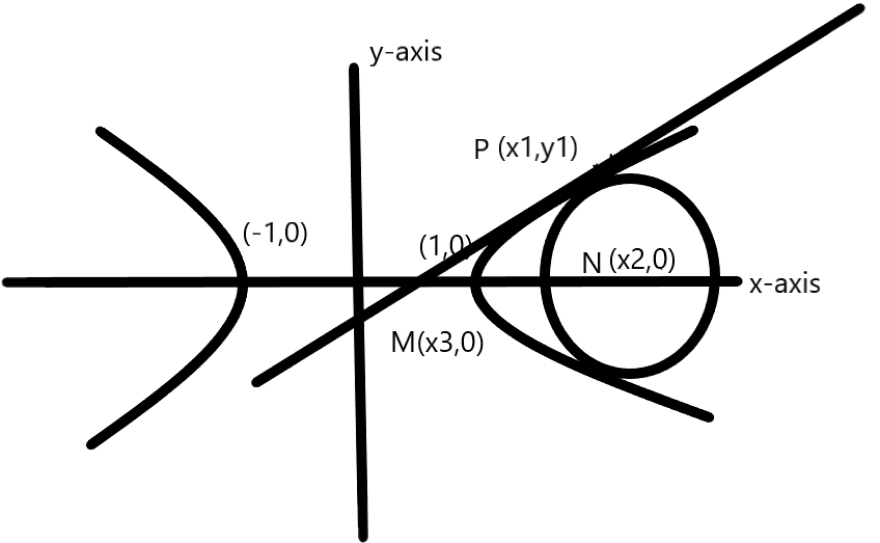



Consider The Hyperbola Hx2 Y2 1 And Circle S With The Class 11 Maths Cbse
Find the exact average value of \(g(x,y) = \sqrt{x^2 y^2}\) over the interior of the circle \(x^2 (y1)^2 = 1\text{}\) Find the volume under the surface \(h(x,y) = x\) over the region \(D\text{,}\) where \(D\) is the region bounded above by the line \(y=x\) and below by the circle (this is the shaded region in Figure 1154)X 4 2 y 6 2 = 49;Thus, the equation of the circle 1
Example 1 Find the points of intersection of the circles given by their equations as follows (x 2) 2 (y 3) 2 = 9 (x 1) 2 (y 1) 2 = 16 Solution to Example 1 We first expand the two equations as follows x 2 4x 4 y 2 6y 9 = 9 x 2 2x 1 y 2 2y 1 = 16 Multiply all terms in the first equation by 1 to obtain an equivalent equation and keep the second equation13 Let F=2xiyj and let n be the outward uni normal vector to the positively oriented circle x2y2=1Compute the flux integral F⋅nds C ∫ Method 1 You can use Gauss' Divergence Theorem F⋅nds=∇⋅FdA S ∫∫ C ∫ F⋅nds=(21)dA S ∫∫∫=3π Method 2 ∫(2x,y)⋅(x,y)ds=∫2xdyy(−dx) x=cosθ y=sinθ ds=rdθ ⇒ ds=dθ because the radius is 1 dx=−ydθ dy=cosθdθTherefore the circle $$\{(x,y) \in \b R^2 x^2 y^2 = 1\} = f^{1}(\{1\})$$ is closed in $\b R^2$ Your set is also bounded, since, for example, it is contained within the ball of radius $2$ centered at the origin of $\b R^2$ (in the standard topology of $\b R^2$) Since $\{(x,y) \in \b R^2 x^2 y^2 = 1\}$ is a closed and bounded
X162 Line Integrals Example 1 Evaluate Z C (2 x2y) ds, where C is the upper half of the unit circle x2 y2 = 1 Solution the half circle can be parametrized by (x = cost, y = sint,How to determine the equation of a tangent Determine the equation of the circle and write it in the form ( x − a) 2 ( y − b) 2 = r 2 From the equation, determine the coordinates of the centre of the circle ( a;X^2y^2=1 radius\x^26x8yy^2=0 center\ (x2)^2 (y3)^2=16 area\x^2 (y3)^2=16 circumference\ (x4)^2 (y2)^2=25 circlefunctioncalculator x^2y^2=1 en




C Is The Circle With The Equation X 2 Y 2 1 Brainly Com



How Do You Determine The Domain And Range Of The Relation X 2 Y 2 1 And X 2 Y 2 100 I Know It Makes A Circle But I M Just Confused About The Enotes Com
Example 1 Find the area enclosed by the circle 𝑥2 𝑦2 = 𝑎2 Drawing circle 𝑥^2 𝑦^2= 𝑎^2 Center = (0, 0) Radius = 𝑎 Hence OA = OB = Radius = 𝑎 A = (𝑎, 0) B = (0, 𝑎) Since Circle is symmetric about xaxis and yaxis Area of circle = 4 × Area of Region OBAO = 4 ×X r 2 y r 2 = 1 The unit circle is stretched r times wider and r times taller University of Minnesota General Equation of an Ellipse Stretching, Period and Wavelength y = sin(Bx) The sine wave is B times thinner Period (wavelength) is divided by B Frequency is multiplied by B For the following exercises, evaluate the line integrals by applying Green's theorem 1 ∫C2xydx (x y)dy, where C is the path from (0, 0) to (1, 1) along the graph of y = x3 and from (1, 1) to (0, 0) along the graph of y = x oriented in the counterclockwise direction 2 ∫C2xydx (x y)dy, where C is the boundary of the region lying




Example 10 Find Area Enclosed Between Two Circles X2 Y2 4




Example 1 Find Area Enclosed By Circle X2 Y2 Examples
Find the centre and radius of the circles if equation of circles is givenWell the standard form of a circle is x minus the x coordinate of the center squared, plus y minus the y coordinate of the center squared is equal to the radius squared So x minus the x coordinate of the center So the x coordinate of the center must be negative five Cause the way we can get a positive five here's by subtracting a negative fiveAs the particle traverses circle x 2 y 2 = 4 x 2 y 2 = 4 exactly once in the counterclockwise direction, starting and ending at point (2, 0) (2, 0) Solution Let C denote the circle and let D be the disk enclosed by C The work done on the particle is
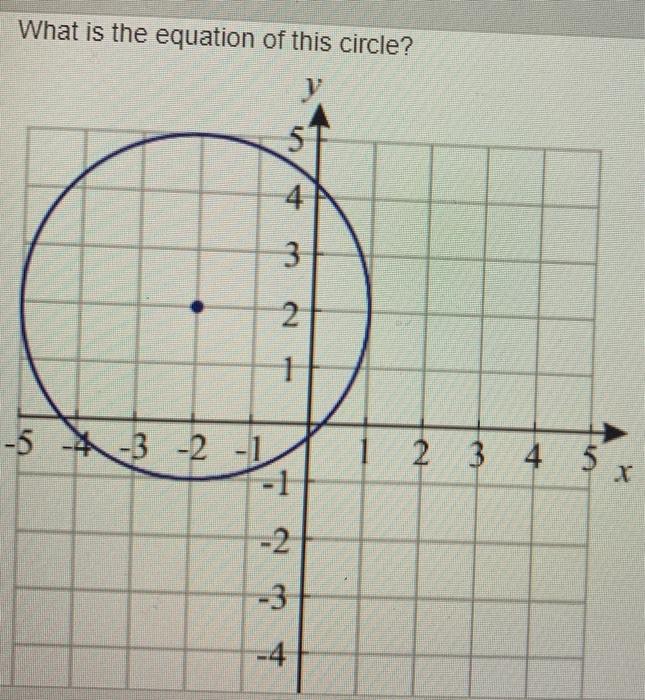



Solved What Is The Equation Of This Circle 4 3 2 1 5 4 3 Chegg Com




A Circle Is Given By X 2 Y 1 2 1 Another Circle C Touches It Externally And Also Touches The X Axis Find The Locus Of The Centre Mathematics Stack Exchange
Find the Center and Radius x^2 (y1)^2=1 x2 (y − 1)2 = 1 x 2 ( y 1) 2 = 1 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard formAlgebra Graph x^2y^2=1 x2 y2 = 1 x 2 y 2 = 1 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the origin, and k k represents the yoffset from origin θ y = r sin θ r 2 = x 2 y 2 We are now ready to write down a formula for the double integral in terms of polar coordinates ∬ D f (x,y) dA= ∫ β α ∫ h2(θ) h1(θ) f (rcosθ,rsinθ) rdrdθ ∬ D f ( x, y) d A = ∫ α β ∫ h 1 ( θ) h 2 ( θ) f ( r cos
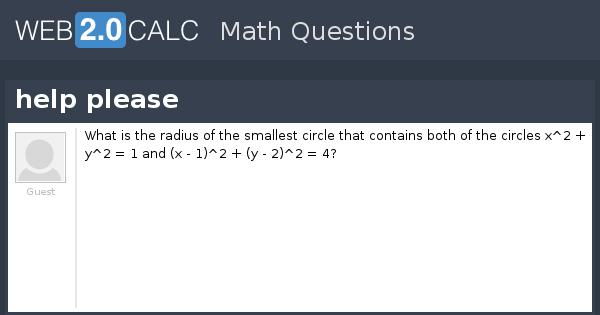



View Question Help Please




With The Help Of A Diagram Explain Why X 2 Y 2 1 Can Be Used To Determine Whether Or Not A Point Lies On The Unit Circle Study Com
Solve the above equation for y y = ~mn~ √ a 2 x 2 The equation of the upper semi circle (y positive) is given by y = √ a 2 x 2 = a √ 1 x 2 / a 2 We use integrals to find the area of the upper right quarter of the circle as follows (1 / 4) Area of circle = 0 a a √ 1 x 2 / a 2 dx Let us substitute x / a by sin t so thatX 5 2 y 9 2 = 81;\displaystyle{3}{x}^{{2}}{y}^{{2}}{2}{x}{2}{y}={0} is an ellipse Explanation Let the equation be of the type \displaystyle{A}{x}^{{2}}{B}{x}{y}{C}{y}^{{2}}{D




Circles



Find The Area Of The Region Enclosed Between The Two Circles X 2 Y 2 1 And X 1 2 Y 2 1 Sarthaks Econnect Largest Online Education Community
B) Determine the gradient of the radius m C D = y 2 − y 1 x 2 − x 1PROBLEM 2364 PEYAM RYAN TABRIZIAN Problem The gure shows a xed circle C 1 with equation (x 1)2y2 = 1 and a shrinking circle C 2 with radius r and center the origin P is the point (0;r), Q is the upper point of intersection of the two circles, and R is the point of intersectionLemma 31 Let Cbe the circle with standard equation f(x,y) = x2 y2 2gx2fy c = 0 For every point P = (u,v), f(u,v) is the power of P with respect to the circle The radical axis of two circles is the locus of points with equal powers with respect to the two circles The radical axis of the two circles x2 y2 2g 1x2f1y c1 = 0, x 2y 2g



Question De065 Socratic



Integrate The Differential Equation Xy Y X2 Y2 1 2 Stumbling Robot
This is simplified to obtain the equation of a unit circle Equation of a Unit Circle x 2 y 2 = 1 Here for the unit circle, the center lies at (0,0) and the radius is 1 unit The above equation satisfies all the points lying on the circle across the four quadrantsThe general equation of a circle is x 2y 2gx2fy c = 0, where the centre is given by (−g,−f) and the radius by r = p g2 f2 − c The equation can be recognised because it is given by a quadratic expression in both x and y with no xy term, and where the coefficients of x2 and y2 are equal Example Find the centre and radius of the circleWhere (x, y) is any point on the circle Squaring both sides of the equation, we get the equation of the circle (x h) 2 (y k) 2 = r 2 Notice that if the circle is centered at the origin, (0, 0), then both h and k in the equation above are 0, and the equation reduces to what we got in the previous section x 2 y 2 = r 2




Inside The Unit Circle S X Y X 2 Y 2 1 There Are Three Smaller Circles Of Equal Ra Youtube




Intersection Of X Y Z 0 And X 2 Y 2 Z 2 1 Mathematics Stack Exchange
The standard Cartesian form for the equation of a circle is #(x h)^2 (y k)^2 = r^2" 1"# where #(x, y)# is any point on the circle, #(h, k)# is the center, and #r# is the radius Equation 2 is the same as equation 1 but with the squares expanded and equation 3 is the given equation with some spaces added for missing termsExample Say point (1,2) is the center of the circle and radius is equal to 4 cm Then the equation of this circle will be (x1) 2 (y2) 2 = 4 2 (x 2 −2x1)(y 2 −4y4) =16 X 2 y 2 −2x−4y11 = 0 Function or Not We know that there is a question that arises in case of circle whether being a function or not It is clear that a circleAll equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction y^ {2}8y3210xx^ {2}=0 y 2 − 8 y 3 2 − 1 0 x − x 2 = 0




Do Now Graph The Equation X 2 Y 2 1 Draw And Label The Special Right Triangles What Happens When The Hypotenuse Of Each Triangle Equals 1 Ppt Download




Unit Circle Trigonometry Learning Math Math Concepts
What is the distance between a circle C with equation x 2 y 2 = r 2 which is centered at the origin and a point P ( x 1 , y 1 ) ?The last equation graphs a parabola How To Graph a Circle Equation A circle can be thought of as a graphed line thatThe fourth equation is the familiar slopeintercept form;
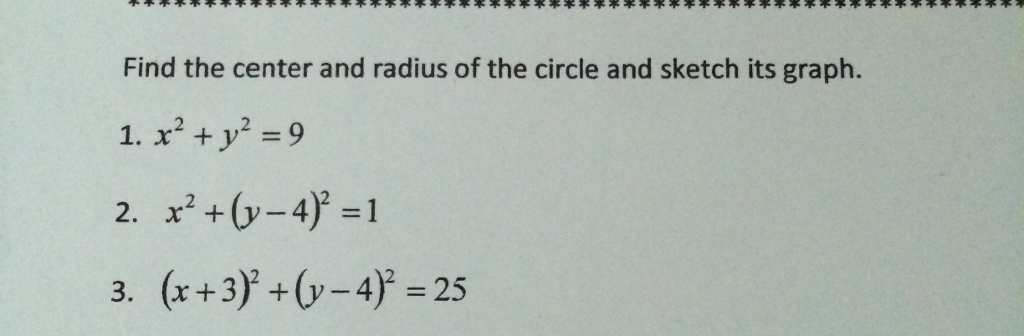



Solved Find The Center And Radius Of The Circle And Sketch Chegg Com




2 1 Plot Of Circle X 2 Y 2 1 And The Definitions Of Cos 8 And Sin Download Scientific Diagram
Answer (1 of 10) Math questions like this one only require that you check the relevant definitions A circle is defined as the set of all points in two dimensions equidistant from a fixed point (called the center) So for any r\in \mathbb R, is the set of points, (x,y), that satisfy x^2y^2=r^2Y)on C through the relation r = h x;T 0, 2 We apply the same procedure to eliminate the parameter, namely square x and y, and add the terms x 2 y 2 = sin 2 (t) cos 2 (t) = 1




Find A Parameterization For The Circle X 2 2 Y 2 1 Starting At The Point 1 0 And Moving Clockwise Twice Around The Circle Using The Central Angle 0 In The Figure Below



Solution X 2 Y 2 9 0 List The Domain Range Center And Radius
Y′ = xy(1−x2 −y2) Figure 2 shows how the associated velocity vector field looks on two circles On a circle of radius 2 centered at the origin, the vector field points inwards, while on a circle of radius 1/2, the vector field points outwards To prove this, we write the vector field along a circle of radius r as (3) x′ = (−yi(x−0) 2 (y−0) 2 = 1 2 x 2 y 2 = 1 Which is the equation of the Unit CircleRadius\x^2y^2=1 radius\x^26x8yy^2=0 radius\ (x2)^2 (y3)^2=16 radius\x^2 (y3)^2=16 radius\ (x4)^2 (y2)^2=25 circlefunctionradiuscalculator radius x^2y^2=1 en




Circle Equation More Examples




Consider The Hyperbola Hx2 Y2 1 And Circle S With The Class 11 Maths Cbse
X2 32 y2 22 = 1, so, x = 3 r 1 − y2 22 In y ∈ 0,2, holds 0 6 x The upper limit comes from y = 2 1 − x 3 , that is, x = 3 1 − y 2 We then conclude I = Z 0 −2 Z 3 q 1−y 2 2 2 0 f (x,y) dx dy Z 2 0 Z 3(1−y) 0 f (x,y) dx dy C Areas as double integrals (Section 153) Example Compute the are of the region on the xyplaneX 2 y 2 = cos 2 (t) sin 2 (t) = 1 This is the equation of the unit circle and so the two parametric equations are a parameterization of the unit circle Now, consider x = sin(t), y = cos(t);Y = x 2 6 x 3;



What Is The Graph Of X 2 Y 2 Z 2 1 Quora




Prove That The Unit Circle X 2 Y 2 1 Is A Closed Set Mathematics Stack Exchange
Y i (2) The co ordinates x and y in (2)are not arbitrary {they are related through equation (1) This means that w e are free to assign a v alue only one of the Find the equation of the tangents to the circle x^2y^2=9 with a slope=1 Implicitly differentiate 2x 2yy' = 0 divide through by 2 x yy' = 0 yy' = x y' = x / y If the slope is 1, then y = x and we can use the equation to find the points where this occursThe square that circumscribes the unit circle can be described using the absolute value function by the equation x − y x y = 2 The term "unit square" usually refers to the square bounded by the xaxis, the yaxis, x = 1 and y = 1 It's given by the equation x − y x y − 1 = 1



Solved If A Tangent To The Circle X 2 Y 2 1 Intersects The Coordinat Self Study 365



What Is The Graph Of X 2 Y 2 Z 2 1 Quora
The ray O P → , starting at the origin O and passing through the point P , intersects the circle at the point closest to PThe circle with equation x^2 y^2 = 1 intersects the line y = 7x 5 at two distinct point A and B Let C be the point at which the positive x axis intersects the circle The ACB is† † margin x 2 y 2 = 80 (4, 8) (1, 2) (4,8) Figure 1391 The circle in Example 1393 Λ Substituting this into g (x, y) = x 2 y 2 = 80 yields 5 x 2 = 80, so x = ± 4 So the two constrained critical points are (4, 8) and (4,8)



How Do You Find The Center And Radius Of The Circle Given X 2 Y 2 144 Socratic
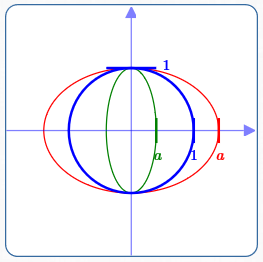



Getting An Ellipse By Stretching Shrinking A Circle
The radius of the circle with the equation (x − 1) 2 (y 2) 2 = 9 is 3 The circle with the equation (x − 1) 2 (y 2) 2 = 9 has centre (1, −2) and radius 3 Lesson Slides The slider below shows another real example of how to find the centre and radius from the equation of a circleFind the length of the chord intercepted by the circle `x^(2) y^(2) 8x 2y 8 = 0 ` on the line `x y 1 =0 `Welcome to Doubtnut Doubtnut is World'sFirst change the disk (x − 1) 2 y 2 = 1 (x − 1) 2 y 2 = 1 to polar coordinates Expanding the square term, we have x 2 − 2 x 1 y 2 = 1 x 2 − 2 x 1 y 2 = 1 Then simplify to get x 2 y 2 = 2 x, x 2 y 2 = 2 x, which in polar coordinates becomes r 2 = 2 r cos θ r 2 = 2 r cos θ and then either r = 0 r = 0 or r = 2 cos θ r = 2 cos θ Similarly, the equation of the paraboloid changes to z




X 2 Y 2 1 Circle Amazingvoice




How To Draw Y 2 X 2 Interactive Mathematics
circle x2 y2 = 4, the cross sections perpendicular to the xaxis are right isosceles triangles with a leg on the base of the solid 13 Picture for Example 4 14 Example 5) Find the volume of the solid whose base is bounded by y = x 1 and y = x21, the cross sections perpendicular to the xaxis are rectangles of height 5 If the circle C 1 x 2 y 2 = 16 intersects another circle C 2 of radius 5 in such a manner that the common chord is of maximum length and has a slope equal to 3/4, then the coordinates of the centre of C 2 are



1



Graphing This Circle Equation X 2 Y 2 14x 4y 0 Mathskey Com



Solution Find The Equation Of The Smaller Circle That Is Tangent To The Axes And The Circle X 2 Y 2 2x 2y 1




The Value Of C For Which X Y 2 Touches Circle X 2 Y 2 2cx 0 And 1 0 Liesinside The Circle Isa 2 B Sqrt 2 1c 2 Sqrt 2 1 D 2 Sqrt 2 1 Snapsolve



1



If The Chord Y Mx 1 Of The Circle X 2 Y 2 1 Subtends An Angle Of Measures 45 Degree At The Major Segment Of The Circle Then Value Of M Is Sarthaks Econnect Largest




Graph X 2 Y 2 4 Youtube




X 2 Y 2 1 Circle Amazingvoice




One End Of A Diameter Of The Circle X2 Y2 3x 5y 4
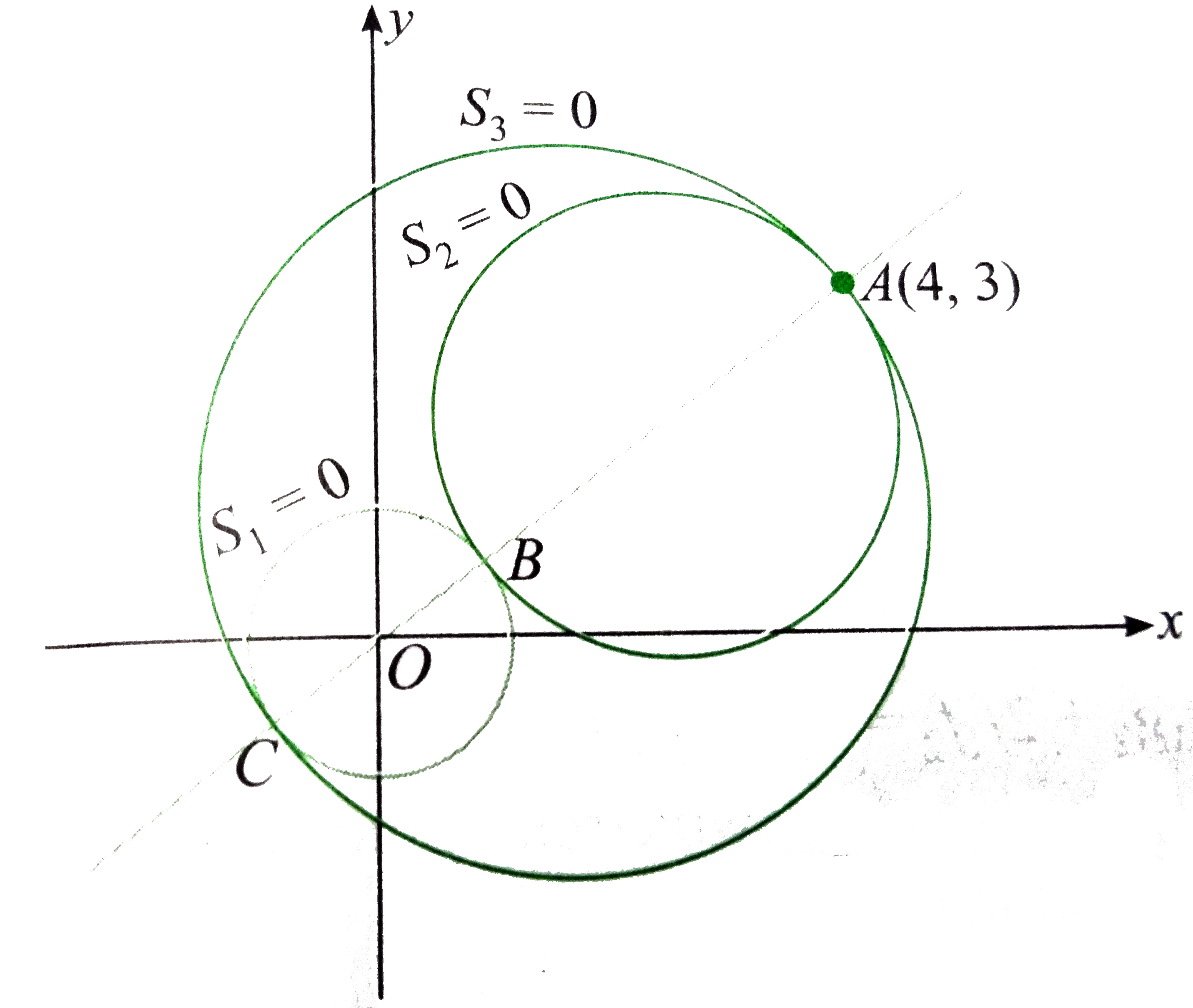



Equation Of The Smaller Circle That Touches The Circle X 2 Y 2



2




Prove That The Radio Of The Circles X 2 Y 2 1 X 2 Y 2 2x 6y 6 0 And X 2 Y 2 4x 12y 9 0 Are In Ap Mathematics Topperlearning Com Sq29gmm



Ellipses And Hyperbolae




Solved Show That The Equation X 2 Y 2 1 2 X 2y 1 16 Chegg Com




X 2 Y 2 1 Circle Amazingvoice



A Circle Is Defined By The Equation Given Below X Gauthmath




For The Points On The Circle X 2 Y 2 2x 2y 1 0 The Sum Of The Maximum And Minimum Values Of 4x 3y Is




X 2 Y 2 1 Circle Amazingvoice
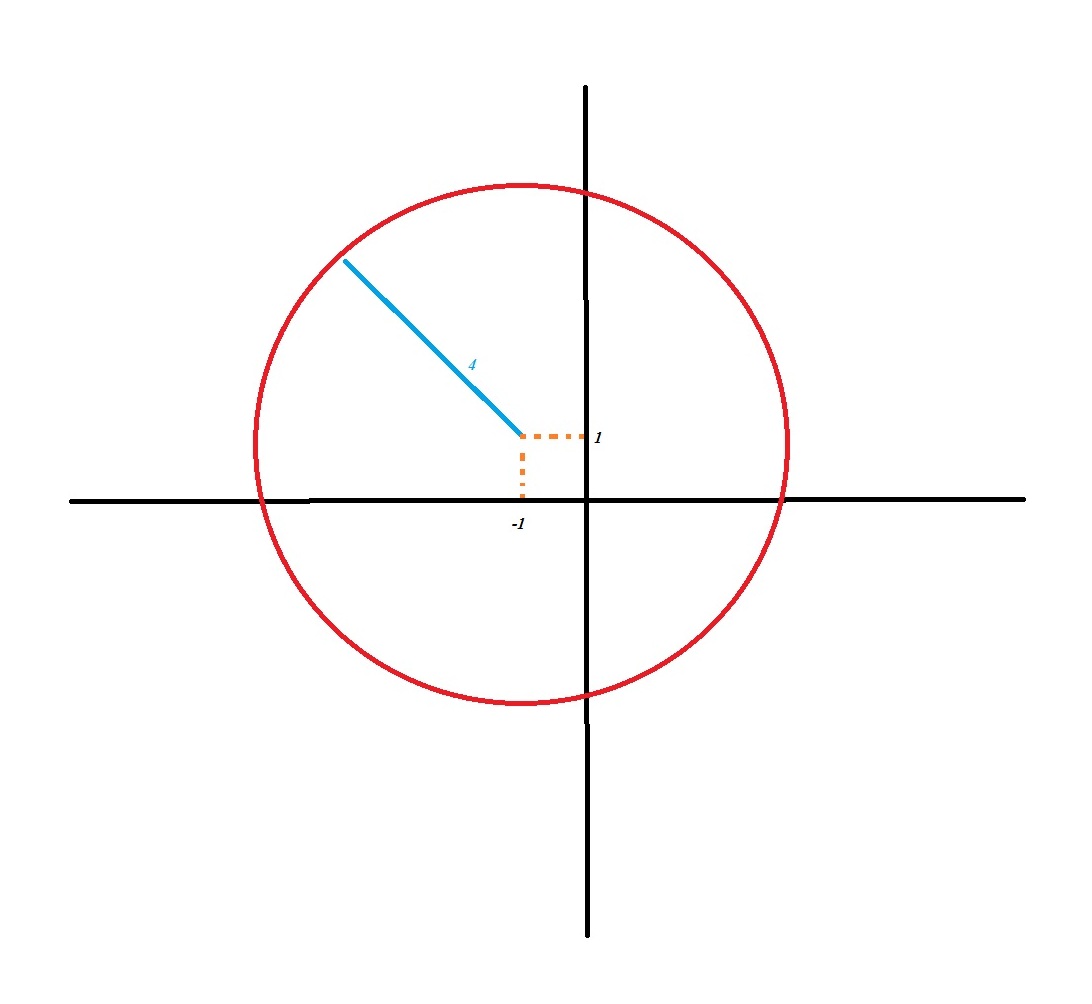



Circle Has The Equation X 2 Y 2 2x 2y 14 0 How Do You Graph The Circle Using The Center H K Radius R Socratic



How Do You Graph X 2 Y 2 1 Socratic




Tangents Are Drawn To The Circle X 2 Y 2 1 At The Points Where It Is Met By The Circles Youtube




Geometry Equations Of A Circle Ppt Video Online Download




Circles Lecture Part 1




10 1 Circles 1 X Y R Higher Maths Lessons Mrthomasmaths X2 Y2 R2 X 2 Y 2 R 2 Youtube




Plotting X 2 Y 2 Z 2 1 Using Matplotlib Without Parametric Form Stack Overflow




Conic Section Wikipedia
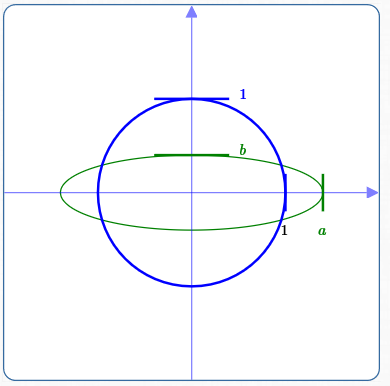



Getting An Ellipse By Stretching Shrinking A Circle




Find The Area Of The Region Inside The Circle X 1 2 Y 2 1 And Outside The Circle X 2 Y 2 1 Study Com



Math Help
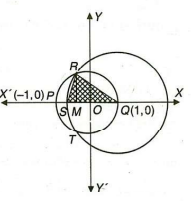



The Circle X 2 Y 2 1 Cuts The X Axis At P And Q Another Circle With Centre At Q And Variable Radius Intersects The Five Circle At R
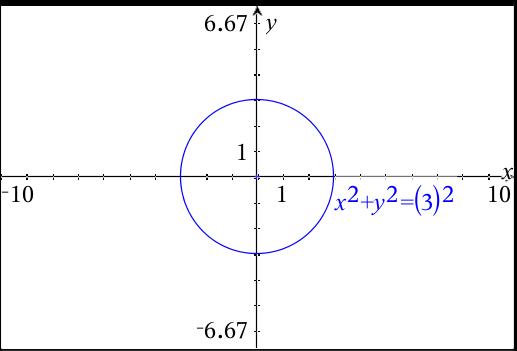



How Do You Graph X 2 Y 2 9 And What Are Its Lines Of Symmetry Socratic




R 2 Circles




The Set X Consists Of All Points Within And On The Unit Circle X



The Normal At The Point 2 3 To The Circle X 2 Y 2 2x 4 Y 3 0 Intersects The Circle X 2 Y 2 1 At Points P And Q



Scarpelli Assignment 2




The Ellipse X 2 A 2 Y 2 B 2 1 Is Such That




Deformation Of The Unit Circle S X 2 Y 2 1 Under The Superflow Download Scientific Diagram




Consider The Circle X 2 Y 2 4x 2y C 0 Whose Centre Is A 2 1 If The Point P 10 7 Is Such That The Line Segment
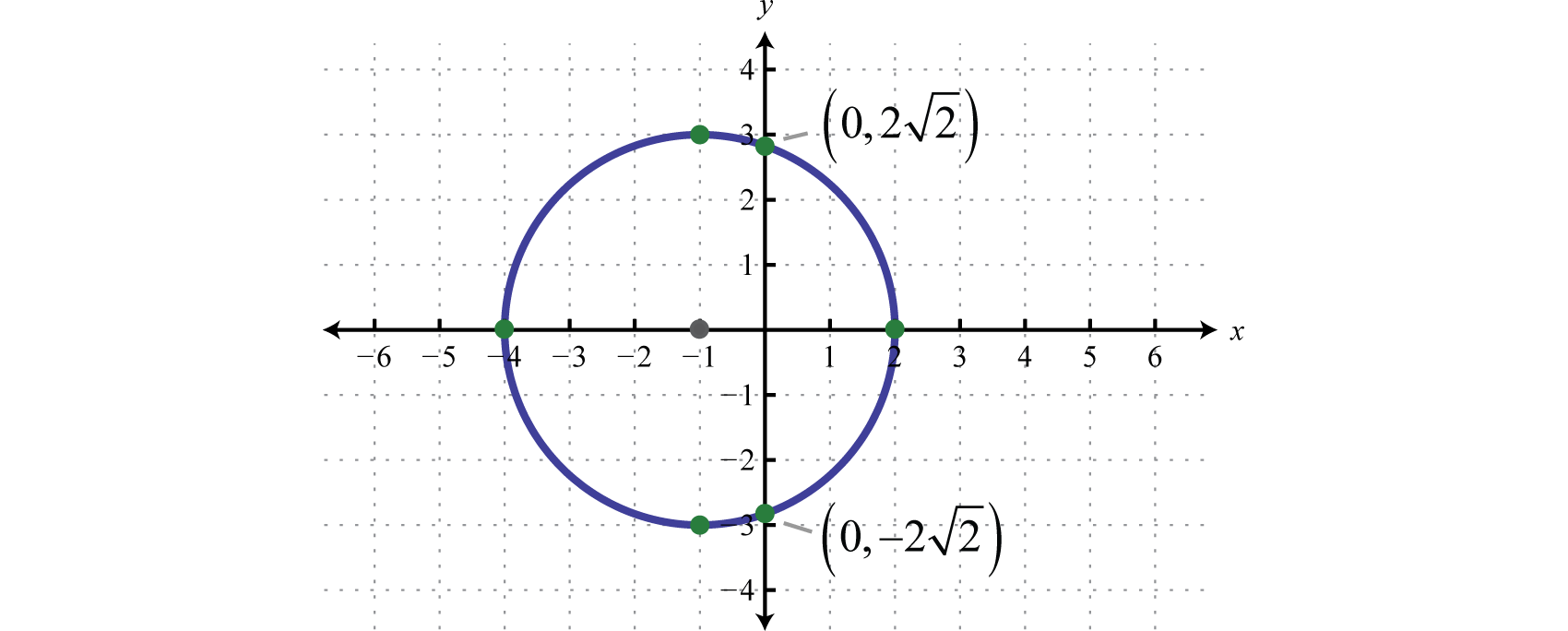



2 8 Circles Mathematics Libretexts




Level Surfaces
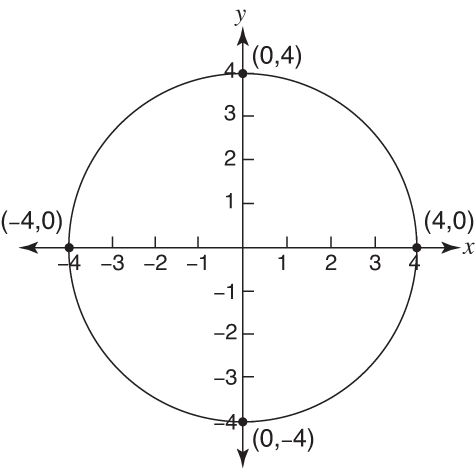



Circle
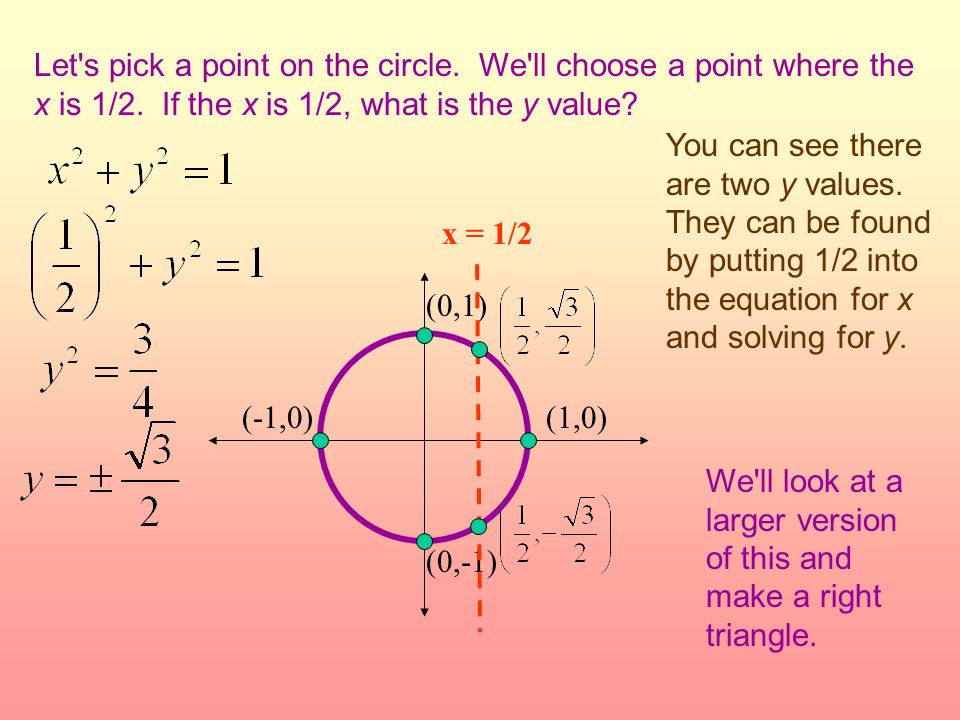



Do Now Given The Equation Of A Circle X 2 Y 2 1 Write The Center And Radius Aim What Is The Unit Circle Hw P 366 4 6 8 10 18 P 367 2 4 6 8 Ppt Download




The Region Inside The Circle X 2 Y 2 A 2 Is Rotated About The X Axis To Generate A Solid Sphere Find Its Volume A Hole Of Diameter A Is Bored Through The



How To Find The Equation Of A Circle With A Radius Of 5 Units And Touches At 1 3 To Another Circle Having Equation X 2 Y 2 14x 10y 26 0 The Required Circle Lies
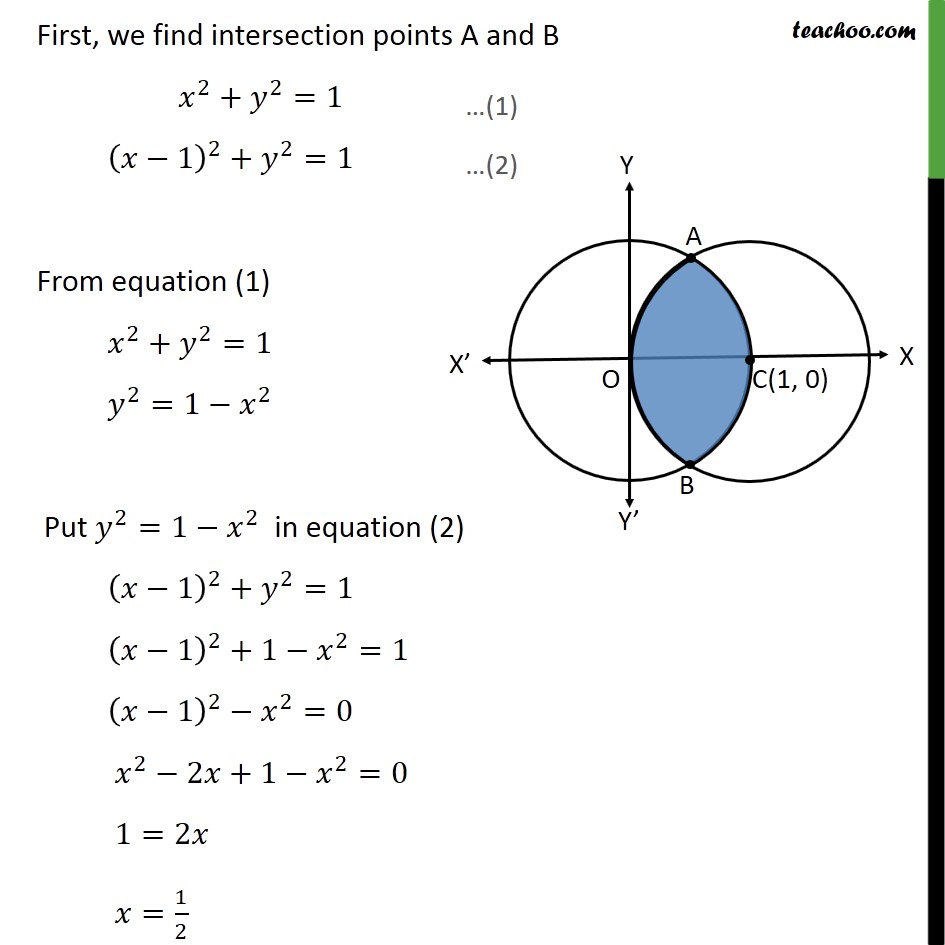



Ex 8 2 2 Find Area Bounded By X 1 2 Y2 1 And X2 Y2 1




Plotting All Of A Trigonometric Function X 2 Y 2 1 With Matplotlib And Python Stack Overflow




5 09 Graphs Of Circles Lesson Mathspace



The Area Of The Region Bounded By The Circle X2 Y2 1 Is Studyrankersonline




Implicit Differentiation
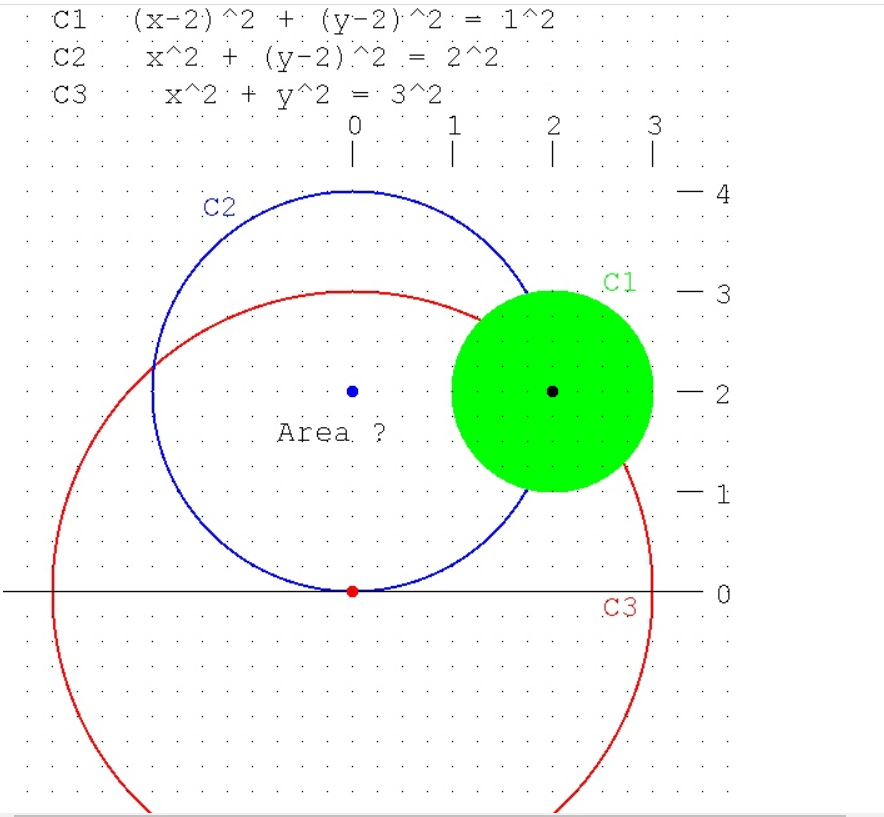



How Do I Find The Area Of The Intersection Of Any Of Chegg Com



Equation Of A




Graph The Circle X 2 Y 2 81 Study Com



How Do You Solve The System X 2y 1 And X 2 Y 2 25 By Graphing Socratic




Ex 8 2 2 Find Area Bounded By X 1 2 Y2 1 And X2 Y2 1




How To Imagine X 2 Y 2 1 0 In C 2 X Y Both Complex Mathematics Stack Exchange




Do Now Graph The Equation X 2 Y 2 1 Draw And Label The Special Right Triangles What Happens When The Hypotenuse Of Each Triangle Equals 1 Ppt Download




Deformation Of The Unit Circle S X 2 Y 2 1 In The Plane Z 1 Download Scientific Diagram
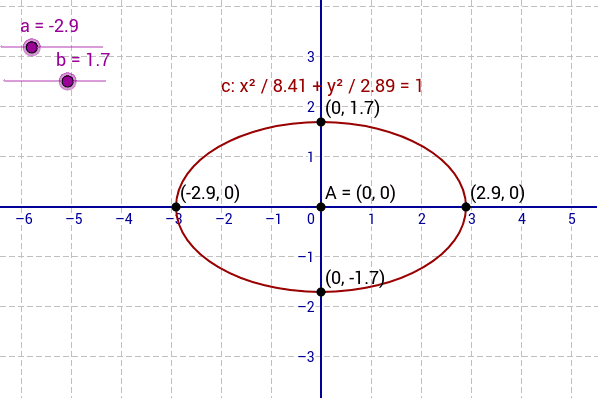



Equation Of An Ellipse X A 2 Y B 2 1 Geogebra



Change Of Variables In Multiple Integrals




Solved Let C1x2 Y2 1c2x 102 Y2 1 And C3x2 Y2 10x 42y 457 0 Be Self Study 365



2
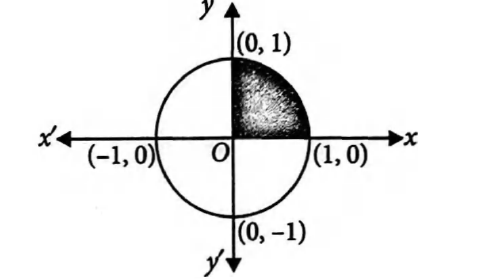



The Area Bounded By The Curve X2 Y2 1 In First Quadrant Is




Is X 2 Y 2 1 Merely Frac 1x Rotated 45 Circ Mathematics Stack Exchange




If The Tangent From A Point P To The Circle X 2 Y 2 1 Is Perpendicular To The Tangent From Youtube




6 A Plot Of The Unit Circle Satisfying X 2 Y 2 1 Download Scientific Diagram
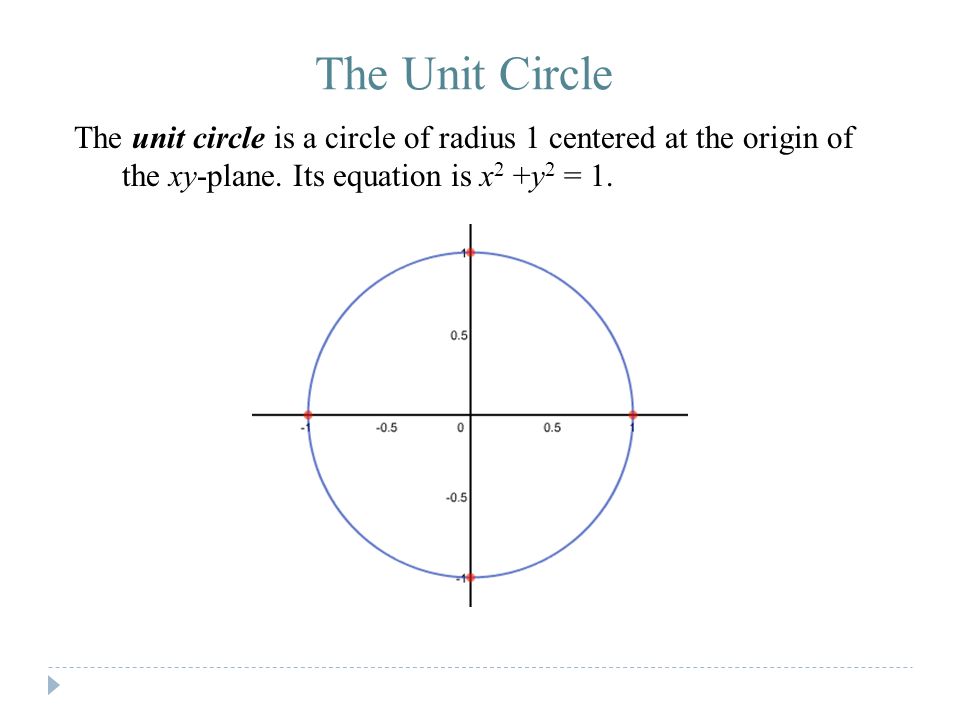



The Unit Circle The Unit Circle Is A Circle Of Radius 1 Centered At The Origin Of The Xy Plane Its Equation Is X 2 Y 2 Ppt Download




8 2 Circles Mathematics Libretexts
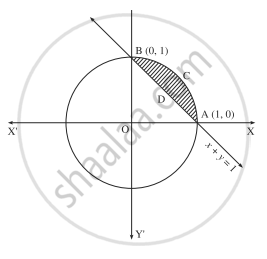



Solve The Following Find The Area Enclosed Between The Circle X2 Y2 1 And The Line X Y 1 Lying In The First Quadrant Mathematics And Statistics Shaalaa Com



Ellipses And Hyperbolae



1




An Example Of A Hyperbola Of Equation X 2 A 2 Y 2 B 2 1 With Download Scientific Diagram



2



What Is The Distance Between Two Points If X Y 1 Cuts Circle X 2 Y 2 1 At Two Points Quora



2



0 件のコメント:
コメントを投稿