三角形の合同条件を考えると、まずひとつ目は 「3組の辺の長さがそれぞれ等しい」 。 ふたつ目は 「2組の辺と、その間の角が等しい」 。 そして最後が 「1組の辺と、その両端の角が等しい」 になります。三角形の合同条件 3組の辺がそれぞれ等しい 2組の辺とその間の角がそれぞれ等しい 1組の辺とその両端の角がそれぞれ等しい これから証明問題へ進んでいく上で 必要となってくるものなので ぜーーーーったいに覚えておきましょう! また、合同な「ハハン、言うまでもなく、三角形の合同条件じゃん。」 なに?! 「言うまでもなく」 な、 キミ! 君は、年寄です( ^^ )。 、、、 今は、 「3辺がそれぞれ等しい。」 「2辺とその間の角がそれぞれ等しい。」 「1辺とその両端の角がそれぞれ等しい
中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su
三角形合同条件 漢字
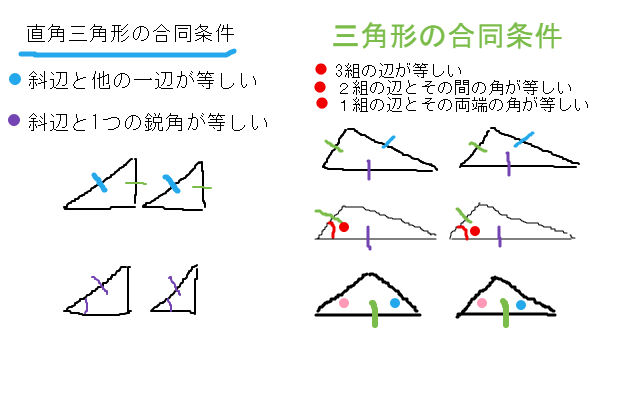
三角形合同条件 漢字-直角三角形の合同条件\(2\) つの直角三角形が合同であることを示したいとき、以下の \(2\) つを利用します。直角三角形の合同条件1 斜辺と \(1\) つの鋭角がそれぞれ等しい。2 斜辺と他の \(1\) 辺がそれぞれ等しいこの \(2\) つは暗記してください。三角形の合同条件 3組の辺がそれぞれ等しい 2組の辺とその間の角がそれぞれ等しい 1組の辺とその両端の角がそれぞれ等しい これらは重要なので3つともきちんと覚えましょう。 特に 「それぞれ」 という語句を忘れがちなので要注意。 どれも 「〇〇が




三角形の合同条件についての質問です 三角形の合同条件で 2つの辺と 数学 教えて Goo
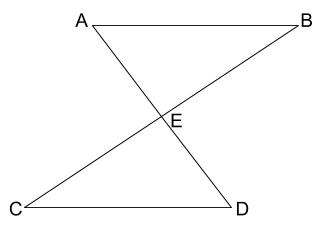
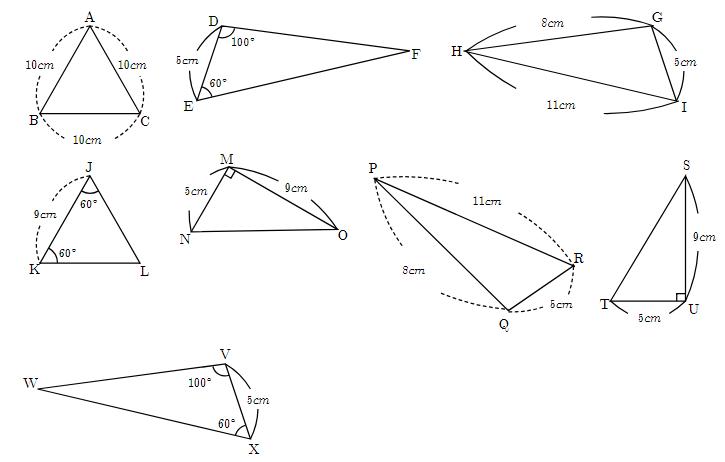
合同条件 「図形の合同#三角形の決定問題」こちらも参照 2 つの三角形を移動して重ねあわせることができるとき、この 2 つの三角形は合同である。ここでいう移動とは、平行移動、回転移動、対称移動を組み合わせたものである。 合同条件を一言一句正確に書くのはもちろん、与えられた問題の文章や図形からどの合同条件に導けばいいのかを意識して問題を解いてみてください。 1下の図で、2つの三角形は合同です。 このとき次の問いに答えなさい。 (1)この2つの三角形が合同直角三角形の合同条件 斜辺と他の1辺がそれぞれ等しい。 斜辺と1つの鋭角がそれぞれ等しい。 『e学ぼ』で三角形の定義と定理を学習! 三角形の定義と定理をきちんと理解して各種の証明問題に役
第1巻命題4 三角形の合同条件(二辺夾角相等) 第1巻 第1巻命題 第1巻命題命題104 公理7 公理9 もし二つの三角形が二辺が二辺にそれぞれ等しく、その等しい二辺に挟まれる角が等しいならば、底辺は底辺に等しく、三角形は三角形に等しく、残りの二角 直角三角形の合同条件 2 2 つの三角形がともに直角三角形であるとわかっている場合は,それらが合同かどうかを確かめることはより簡単になります.つまり,先にみたような一般の三角形に対する合同条件よりも少ない情報で,合同かどうかを確かめる この記事では、「合同」についてわかりやすく解説していきます。 三角形の合同条件や証明問題の解き方も説明していくので、ぜひマスターしてくださいね! 目次 非表示 合同とは? 合同の記号 合同の性質 三角形の合同条件 ① 3 組の辺がそれぞれ
三辺相等は合同の証明 三辺の長さがそれぞれ同じ三角形の1辺を重ね合わせます。 残りの2辺の交点は原論第1巻命題17により、1つに定まります。 2線分の交点が別々の位置にはなりません。 原論公理7より「互いに重なり合うものは互いに等しく」なり次の条件のどれかが成り立つと、$2$ つの三角形は合同であるといえます。 三角形の合同条件 ① $\textcolor{blue}{3}$ 組の辺がそれぞれ等しい。 ② $\textcolor{blue}{2}$ 組の辺とその間の角がそれぞれ等しい。 ③ $\textcolor{blue}{1}$ 組の辺とその両端の角がそれぞれ等しい。 数検1級 三角形と円を題材にして、大きく三角形の合同・三角形の相似・三平方の定理・円の性質を勉強するよ。 最後に行くにつれて簡単に感じると思いますが、数検対応級は 5級 ~ 準2級 です。 数学検定5級合格率75%! 過去問は中学1年生範囲だ




合同条件について Blogskol



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
三角形の合同条件は $3$ つでしたが、"直角三角形"という条件が加わることによって $2$ つ増えました。 これら $5$ つを暗記するだけでは、勉強として不十分です。 「 なぜ直角三角形であれば条件が増えるのか 」いろいろな視点で考えることで、数学力が 12 直角三角形の合同条件 2つの直角三角形は、次のうちどれかに当てはまれば合同です。 ④ 斜辺と1つの鋭角が、それぞれ等しい。 ⑤ 斜辺と他の1辺が、それぞれ等しい。 ということで上記の5つだけは覚えておいてください!まとめ 三角形の合同条件は 3つの辺が等しい 2つの辺が等しく、その間の角が等しい 1つの辺が等しく、その両端の角が等しい のいずれかを満たしていることである。 これを図と数式で示すと次のようになります。 最後までご覧いただきありがとう



2




三角形の合同証明の練習 無料で使える中学学習プリント
三角形の成立条件の証明(必要性) 「三角形が成立する→三角不等式が成立する」を証明します。 寄り道した方が距離が長くなる という直感から明らかっぽいですが,一応きちんと証明しておきます。 証明 3辺の長さが a,\b,\c a, b, c であるような三角 三角形の合同の証明はこの三つの性質を利用して行います。 これら三つの性質を利用した、二つの三角形が合同である条件は次の三つです。 ①'二つの三角形において、三組の辺の長さがそれぞれ等しい。 ②'二つの三角形において、一組の辺の長さが taikon @gomi_tweet2222 塾講バイトやってると三角形の合同条件を 「三辺相当」 「二辺夾角相当」 「一辺両端角相当」 って書くと減点する中学校の先生がいるという話を聞くけど、そういう先生は正直、数学をやめて欲しい。



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典
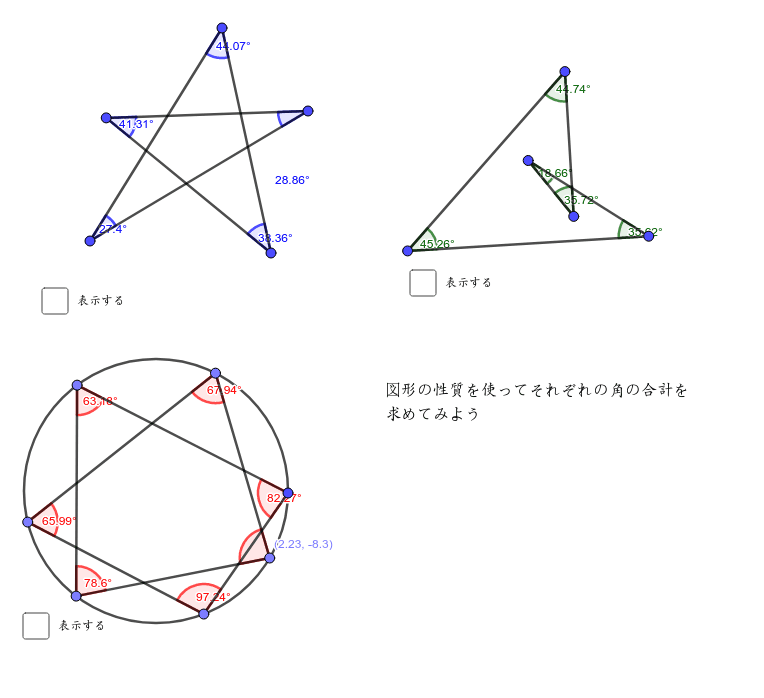



中2 数学 三角形の合同条件 角の和を求めてみよう Geogebra
1三辺の長さがそれぞれ等しい 二つの三角形について、その三辺の長さがそれぞれ等しいとき、二つの三角形は合同であると言えます。 これが一つ目の合同条件です。 おおよそ、以下のような答案を作ることができれば問題ないでしょう。 ABCと A´B´C 今回は「三角形」の合同条件について本気出して考えてみたいと思います。 こうした図形に関する論理や証明といった話題 続きを読む 和から株式会社|大人のための数学教室 三角形の合同条件は以下の3つでした。 ・3つの辺の長さがそれぞれ等しい形になる条件」「平行四辺形の性質」「長方形・ひし形・正方形の関係」)も楽しくできる。 単 元 図形の調べ方 対象学年 2 年 ね ら い 「三角形の合同条件」を知識として定着させ、これからの証明で活用できる ように、ポーカーのルールの要領でカード
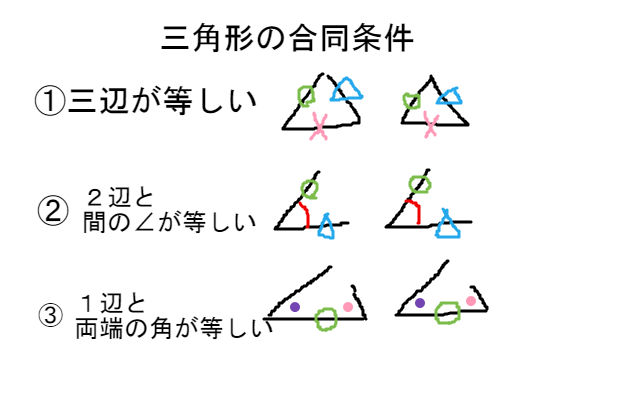



三角形の相似 合同条件 中学 数学 理科の復習サイト




三角形の合同条件 Youtube
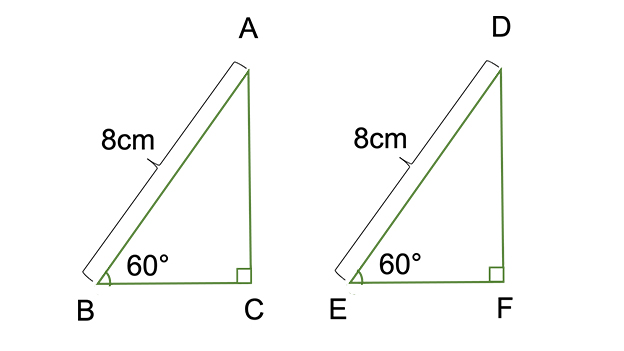
直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき(証明) 2 斜辺と他の1辺が、それぞれ等しいとき(証明)証明)直角三角形の合同条件とは 直角三角形は、以下のことが分かれば合同だと言えます。 今までの三角形の合同条件が このように、3つの情報を組み合わせて合同を言うことができましたが 直角三角形の場合には このように2つの情報だけでOKになります




三角形の合同条件と証明問題の解き方 数学fun




三角形の合同条件 小学生 中学生の勉強



三角形の合同条件 まいにち一題 中学受験過去問題研究



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
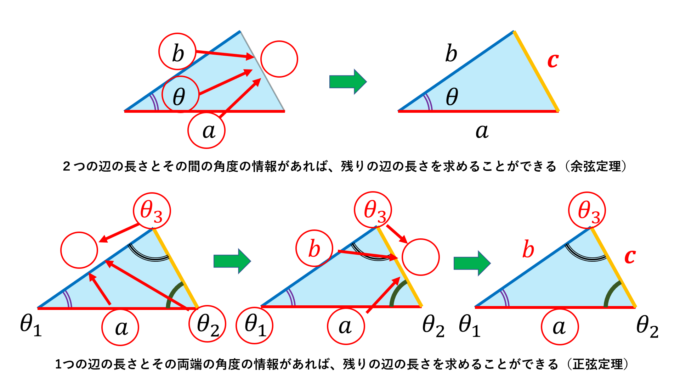



合同条件について本気出して考えてみた 後編 数学 統計教室の和から株式会社
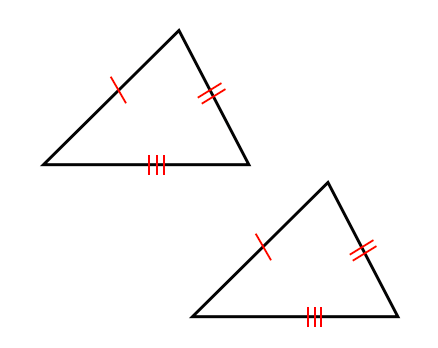



三角形の合同条件を知ろう 苦手な数学を簡単に



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
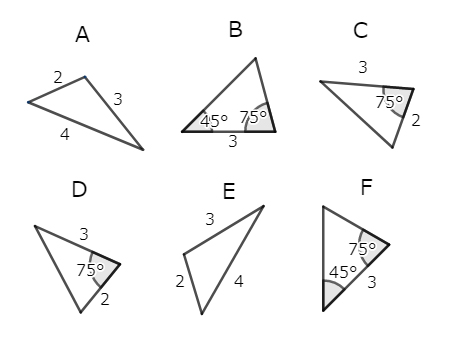



数学のアレ 何に役立つ 三角形の合同条件 同じ形の三角形を見つけて テストで5点くらいもらう 以外の使い方 1 2 ページ ねとらぼ
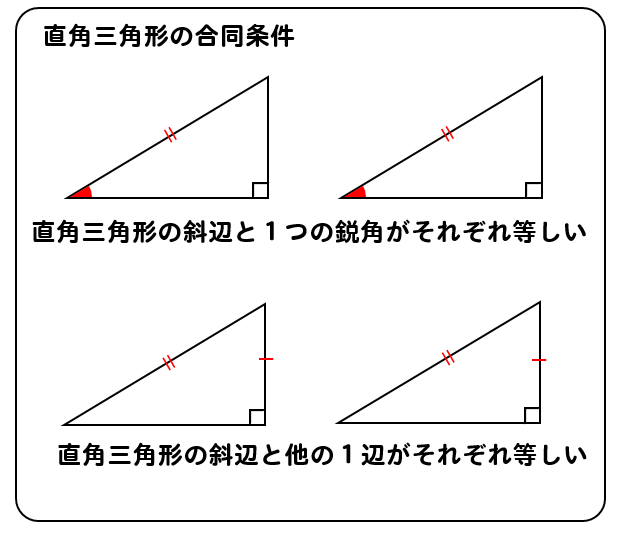



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




中2 直角三角形の合同条件を使った問題にチャレンジ Youtube
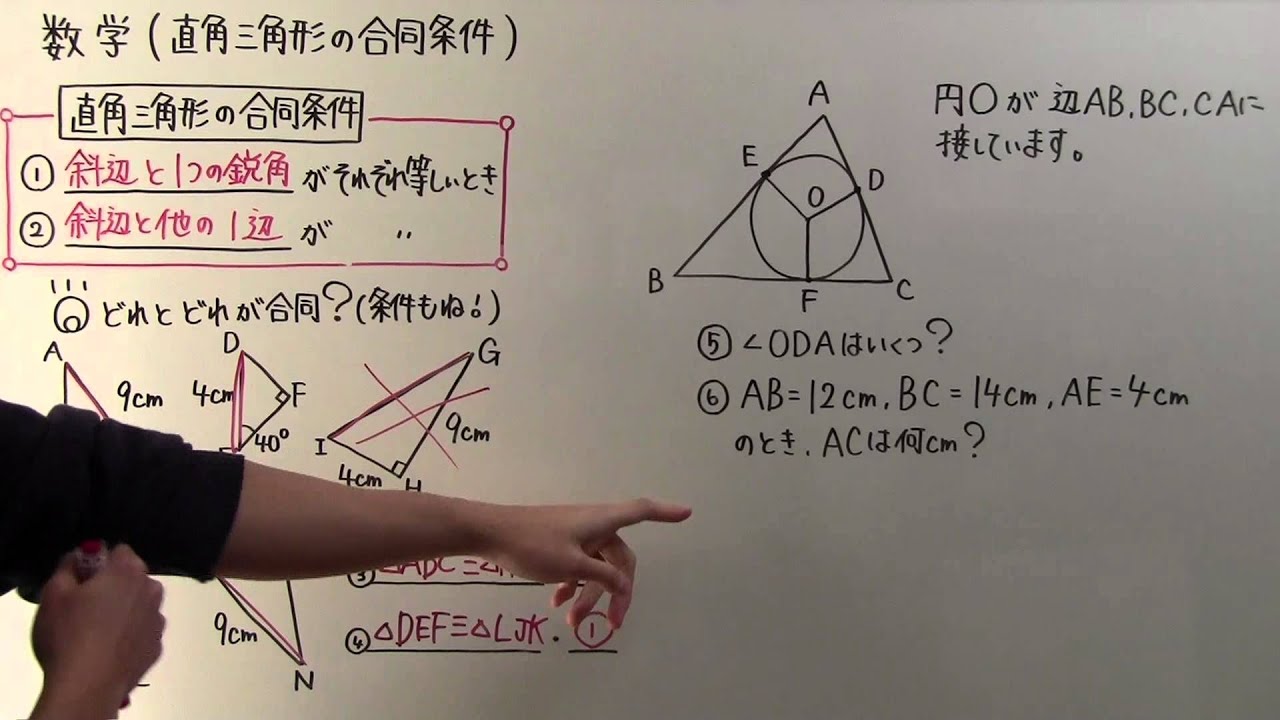



数学 中2 71 直角三角形の合同条件 Youtube
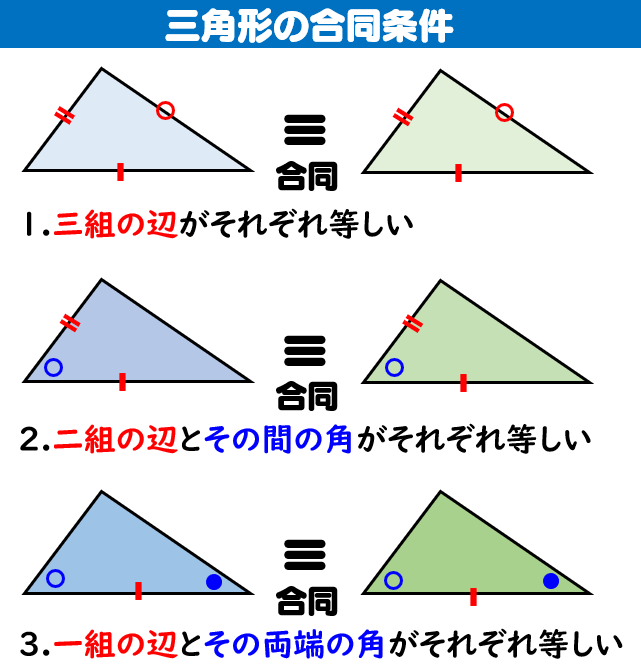



三角形の合同条件と証明問題の解き方 数学fun
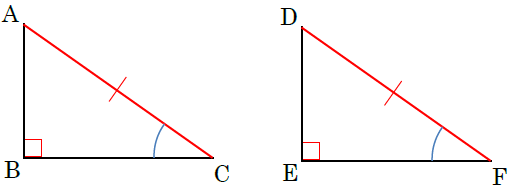



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院




中2 三角形の合同条件の見つけ方 使い方をイチから Youtube




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ



中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋



三角形 合同 相似条件 直角三角形の合同条件 中学 数学 理科の復習サイト



中2数学 三角形の証明の仕方 Pikuu
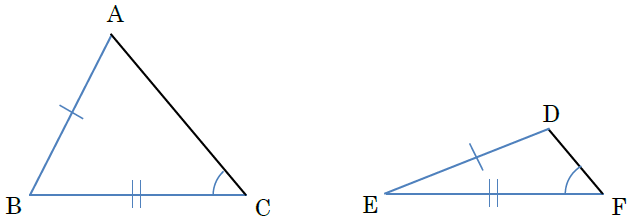



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院
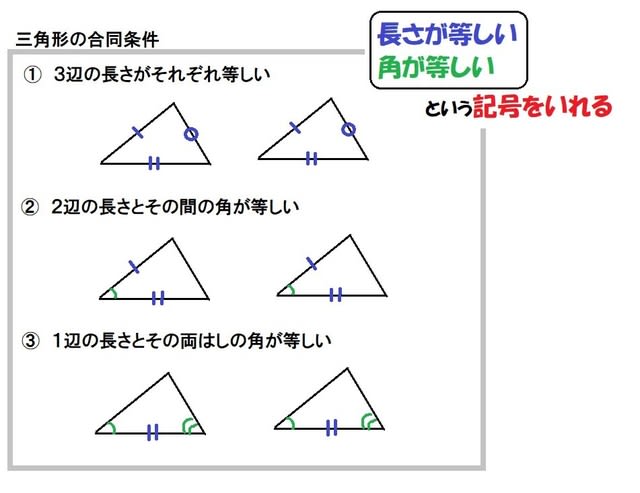



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support




三角形の合同条件と証明問題の解き方 数学fun




三角形の合同条件 証明のときに絶対にしておかないといけない問題 中学や高校の数学の計算問題
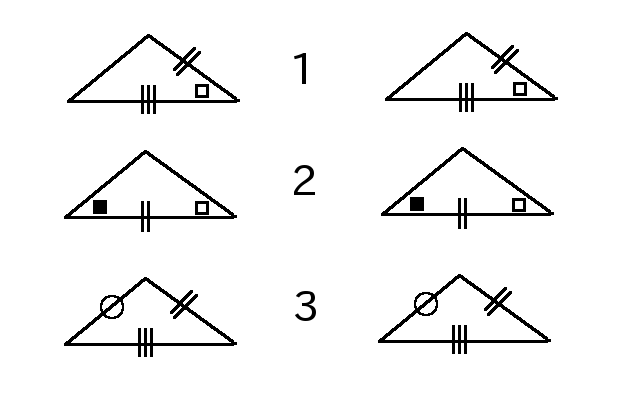



File 三角形の合同条件 Png Wikimedia Commons



1
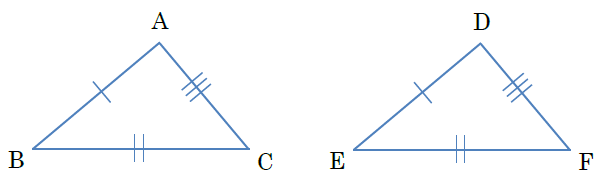



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院
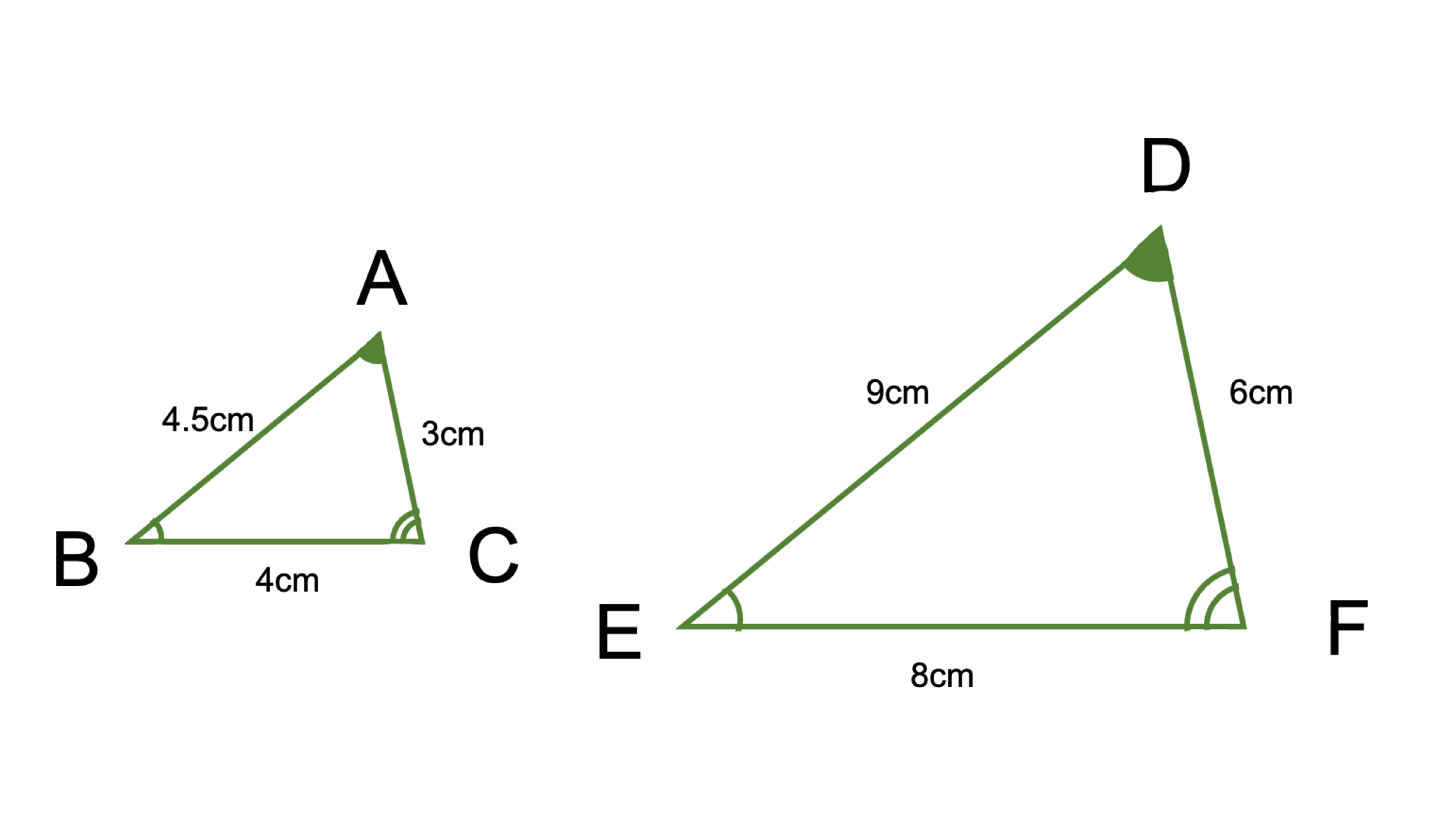



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




中2数学 三角形の合同条件3 1辺とその両端角 映像授業のtry It トライイット
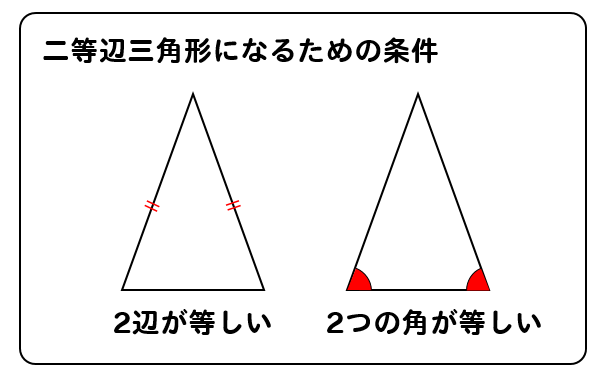



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




中学数学より3 三角形の合同条件 身勝手な主張
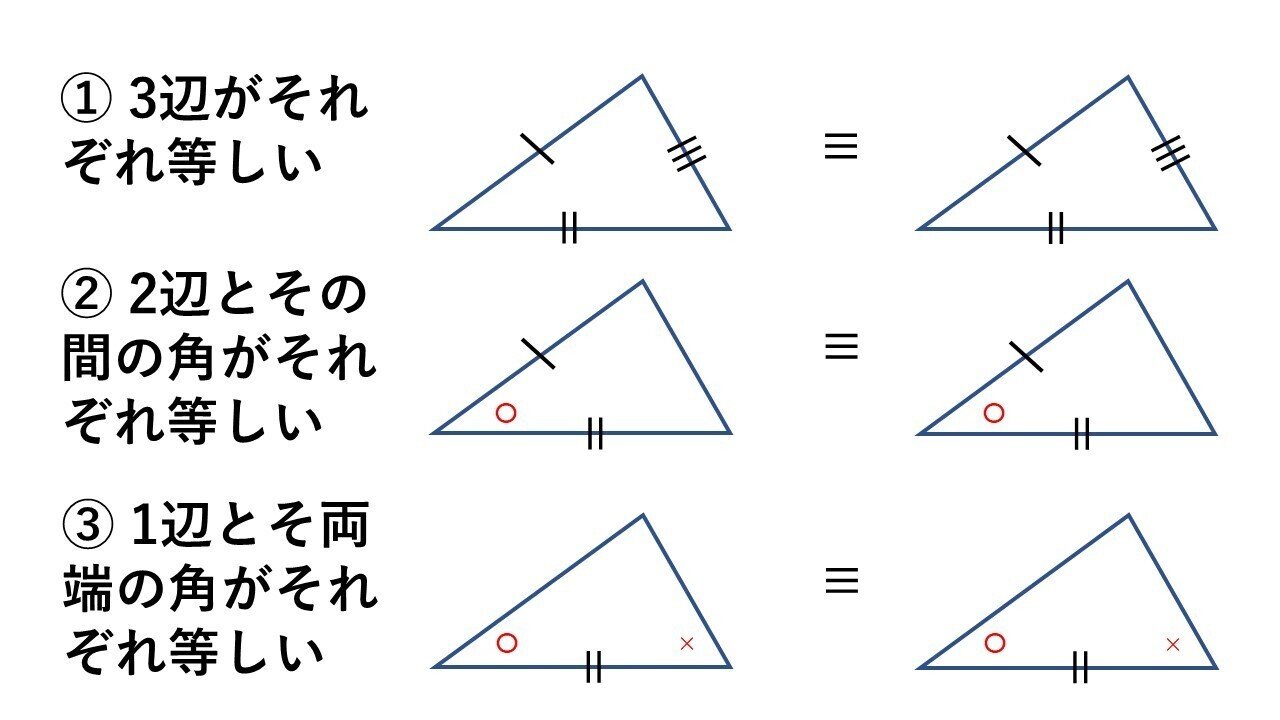



三角形の合同条件から証明へ タロウ岩井のnote Note
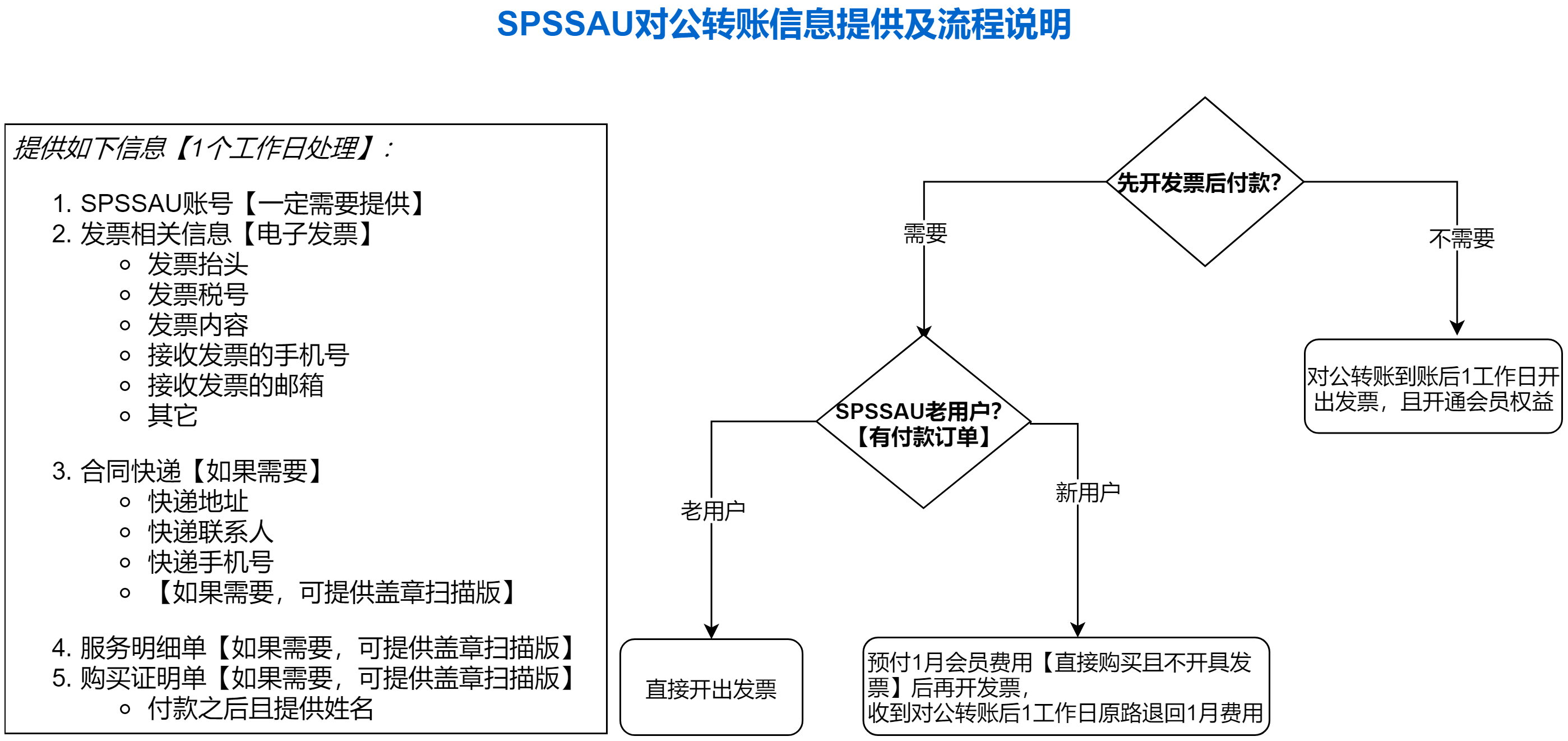



Spss在线 Spssau 发票转账合同等




合同と証明 Ict教材eboard イーボード




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張




三角形の合同条件と証明問題の解き方 数学fun
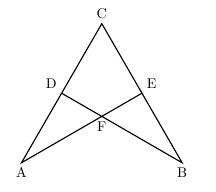



三角形の合同の問題の解法 夢を叶える塾
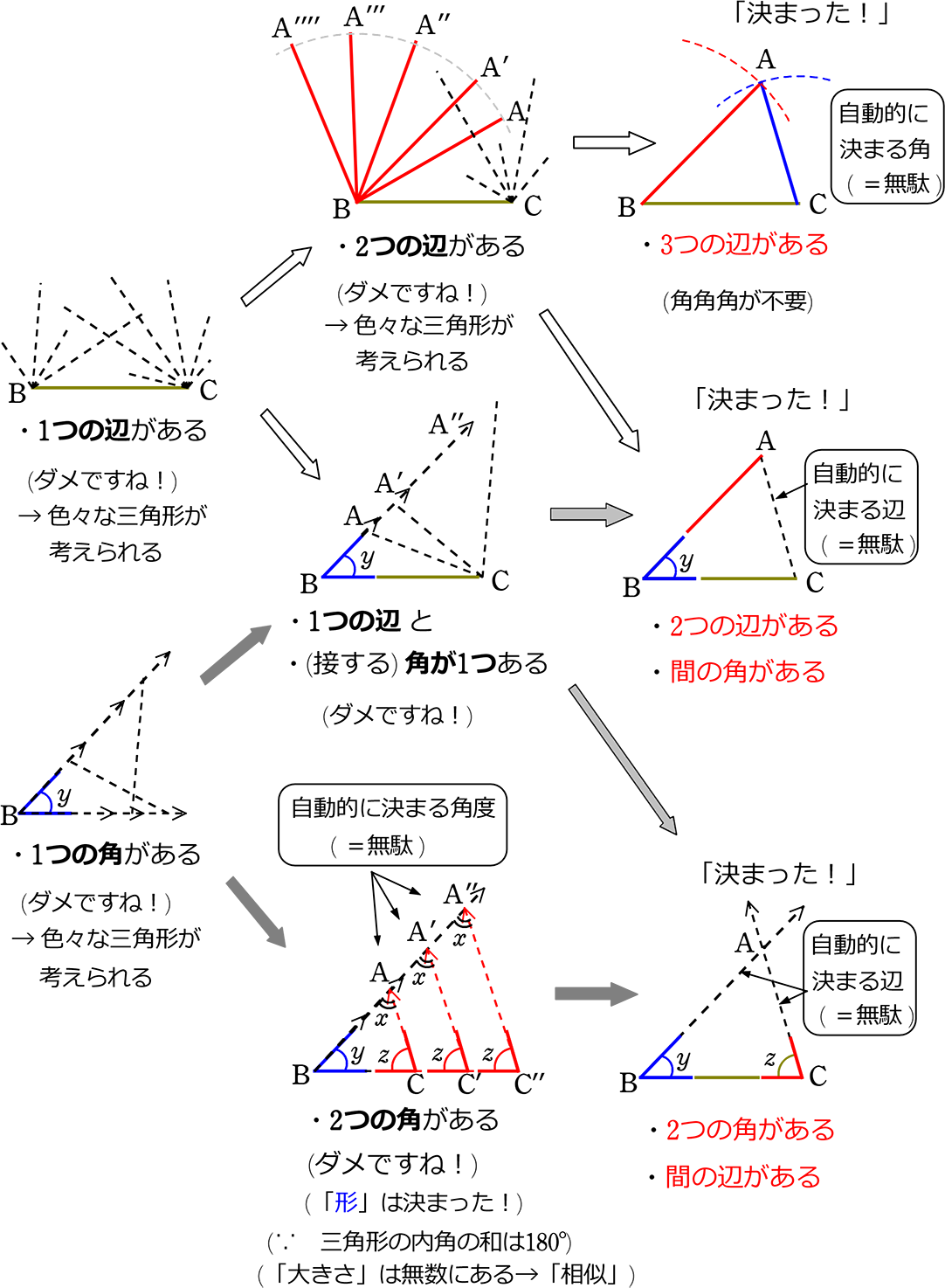



中学数学 図形の合同 図形の性質




直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方



3




中2数学 三角形の合同条件2 2辺とその間の角 例題編 映像授業のtry It トライイット
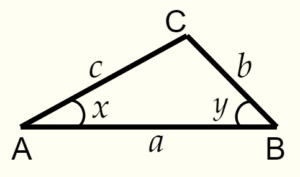



三角形の合同条件を忘れたときは三角形を自分で書いて思い出そう 数学基礎トレーニングルーム



直角三角形の合同条件とそれを利用した証明 チーム エン



1
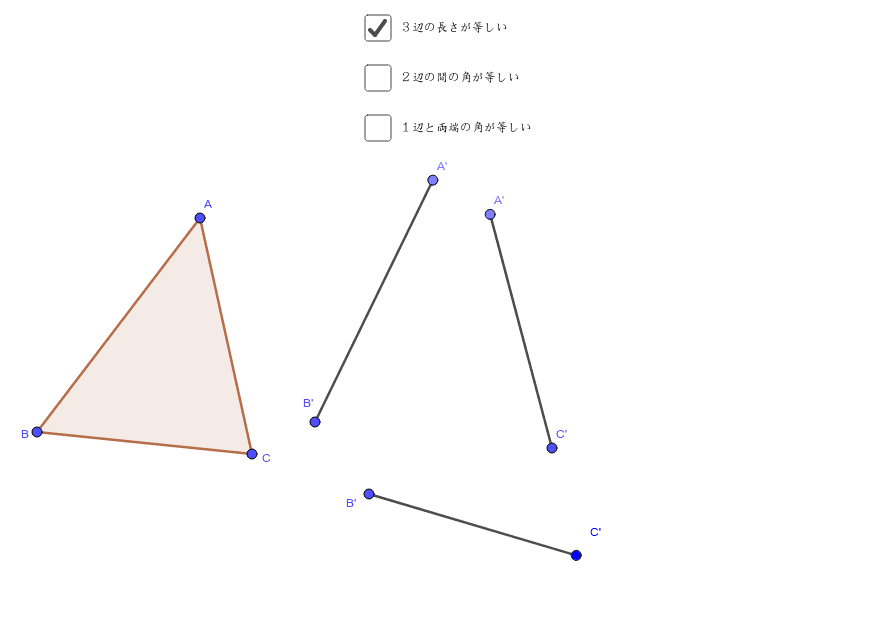



三角形の合同条件 Geogebra




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく
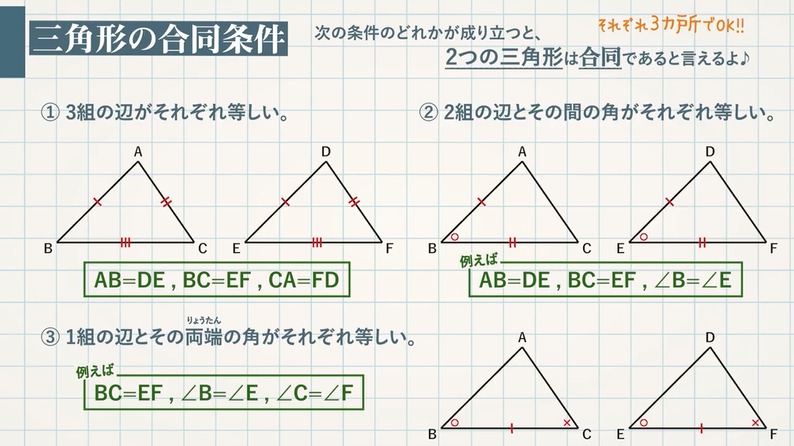



合同な図形とは 三角形の合同条件 教遊者




一瞬だけフォロワーさんが2500人になったシグマゼミ そういや 中2の 三角形の合同条件 とかさ 中学でよくある 一字一句この通りに書かないと減点 なものの代表格だと思うんだけど あれ 教科書によってびみょーにちがったりしないの 写真は 学校




三角形の合同条件についての質問です 三角形の合同条件で 2つの辺と 数学 教えて Goo




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾
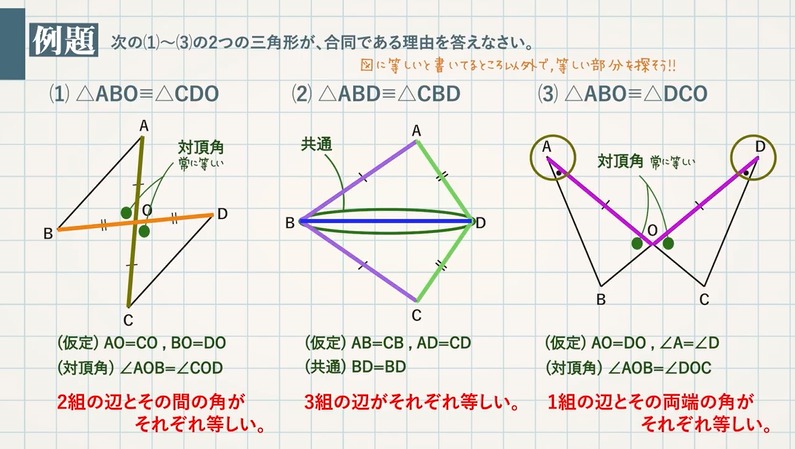



合同な図形とは 三角形の合同条件 教遊者




直角三角形の合同条件再び 中学校2年生の数学 身勝手な主張
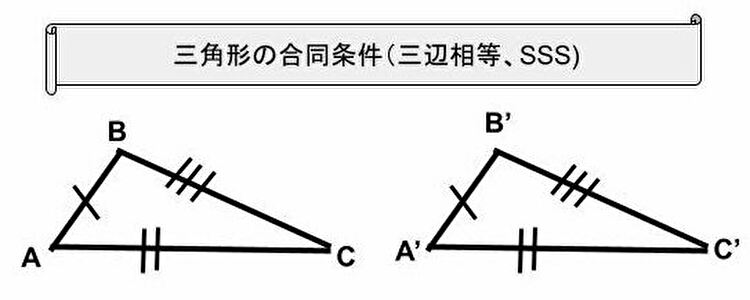



公理から手繰る 三角形の合同条件の証明 三辺相等 Sss 数学探求 ぱるきちどっとこむ



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典




直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題




三角形の合同条件 相似条件と合同条件の違いとは アタリマエ
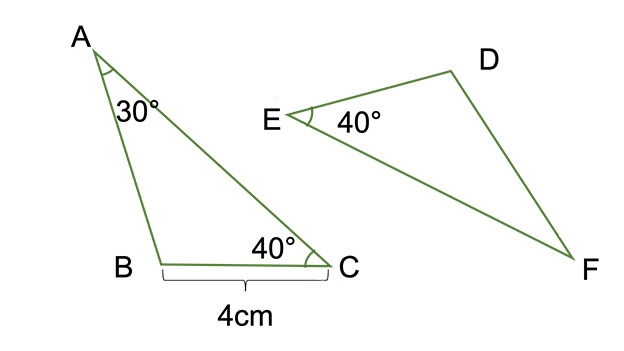



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



2
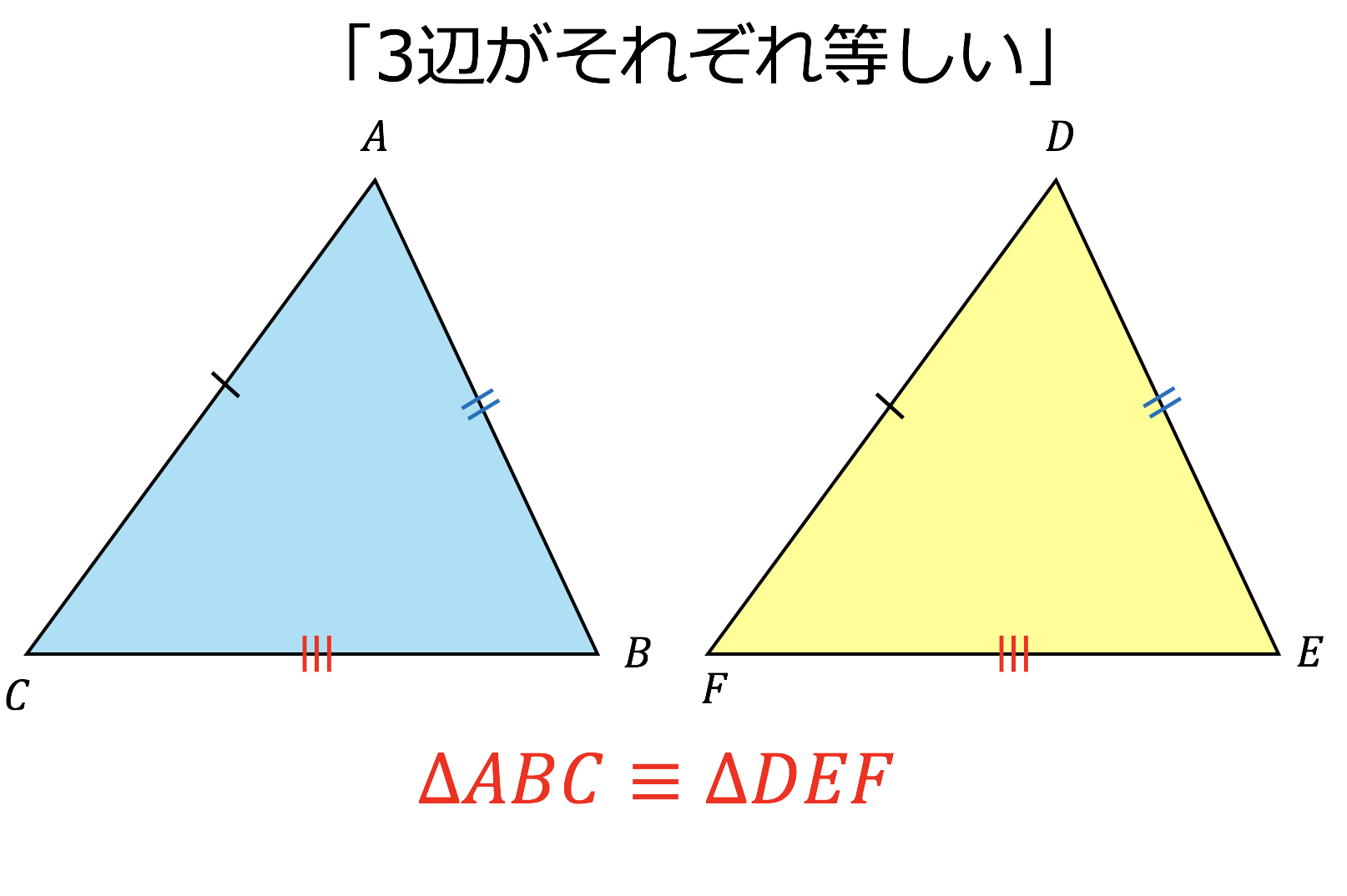



3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ




直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




三角形の合同条件



项目管理 如何让项目重回正轨 悠哉网



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
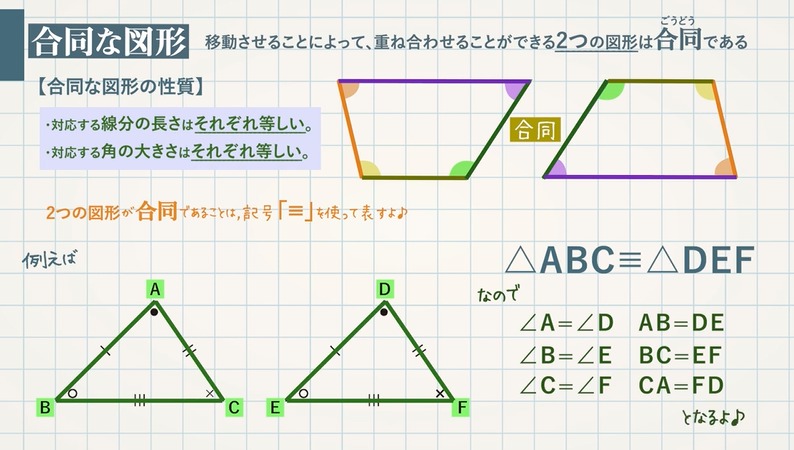



合同な図形とは 三角形の合同条件 教遊者




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院
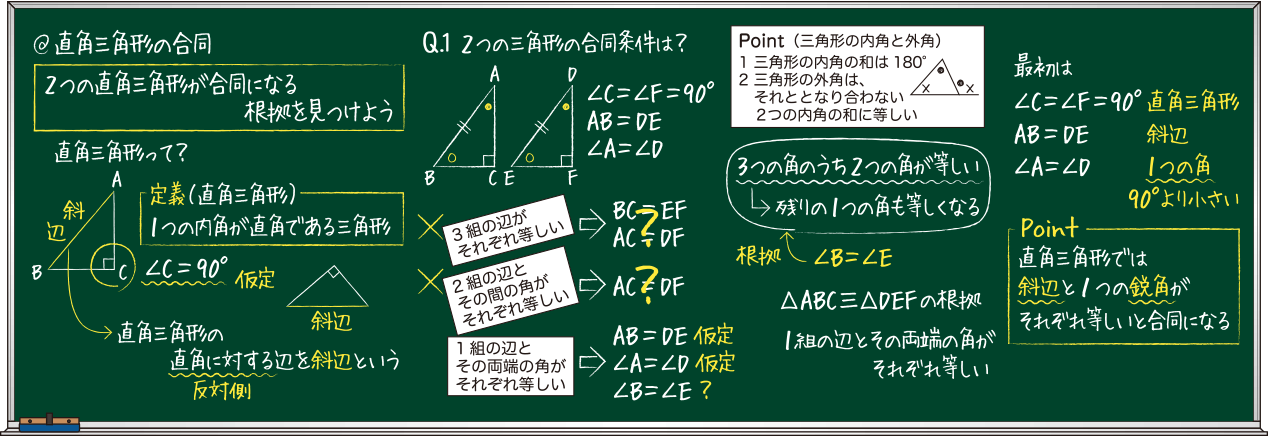



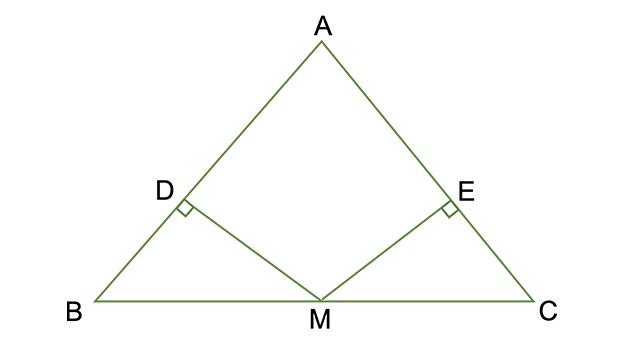
思考を見せる板書例 2年5章 直角三角形になる根拠をみつけよう Math Connect 東京書籍 先生のための算数数学ポータルサイト
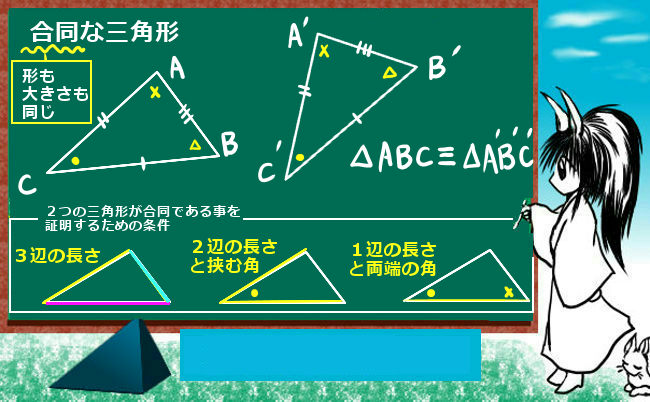



三角形の合同 理数系学習サイト Kori




安全健康的工作条件 业务合作伙伴行为准则 Ericsson




直角三角形の合同条件 算数 数学が好きになりmath
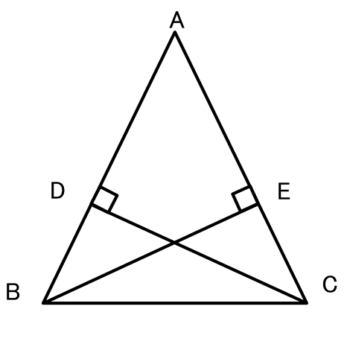



フロー 2 5 4 4 直角三角形の合同条件を利用した証明
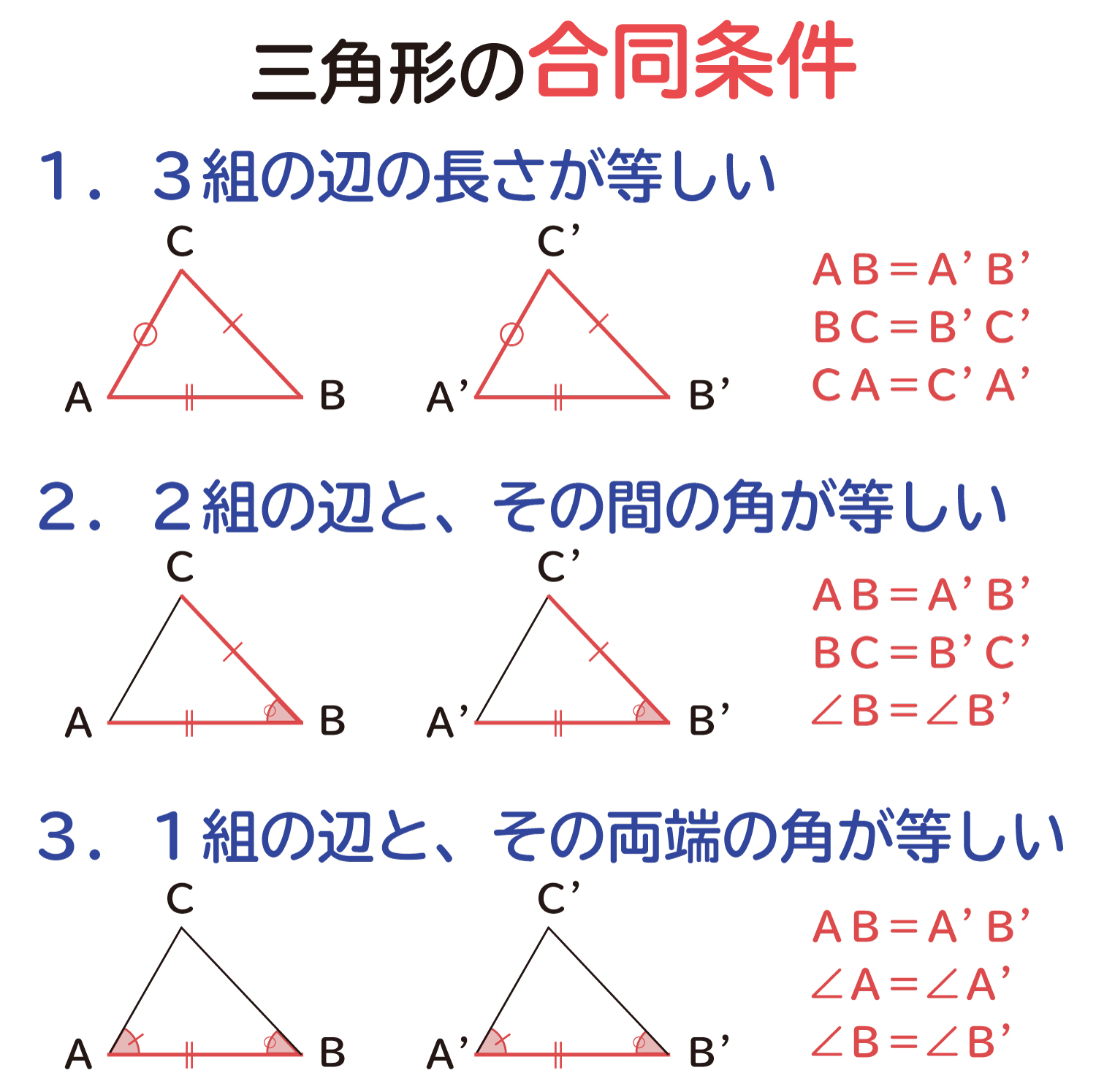



三角形の合同条件の説明 おかわりドリル
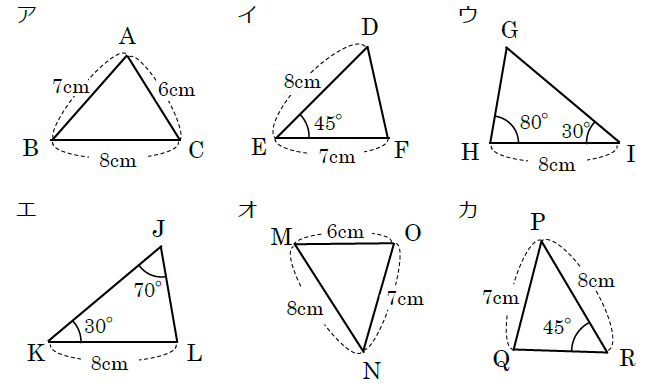



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
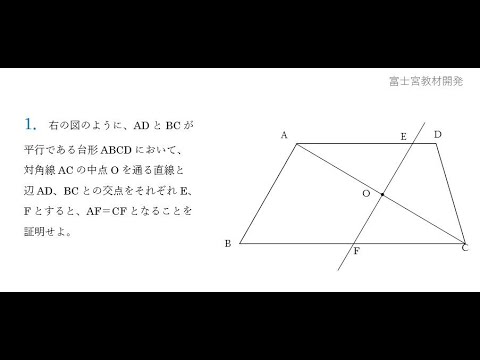



新中学3年生向け 図形の証明 第1講 三角形の合同条件の利用 Youtube
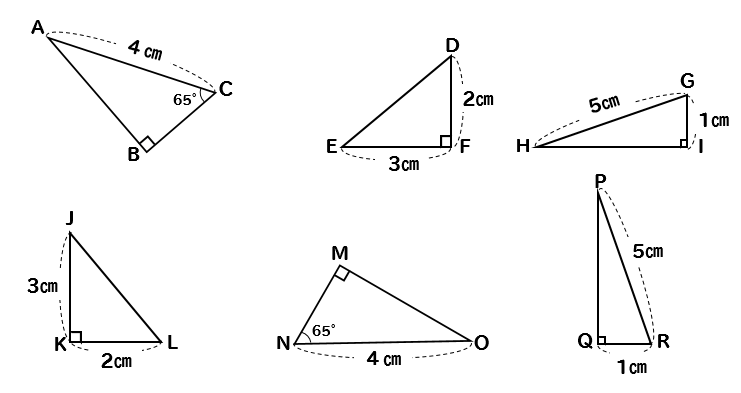



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ
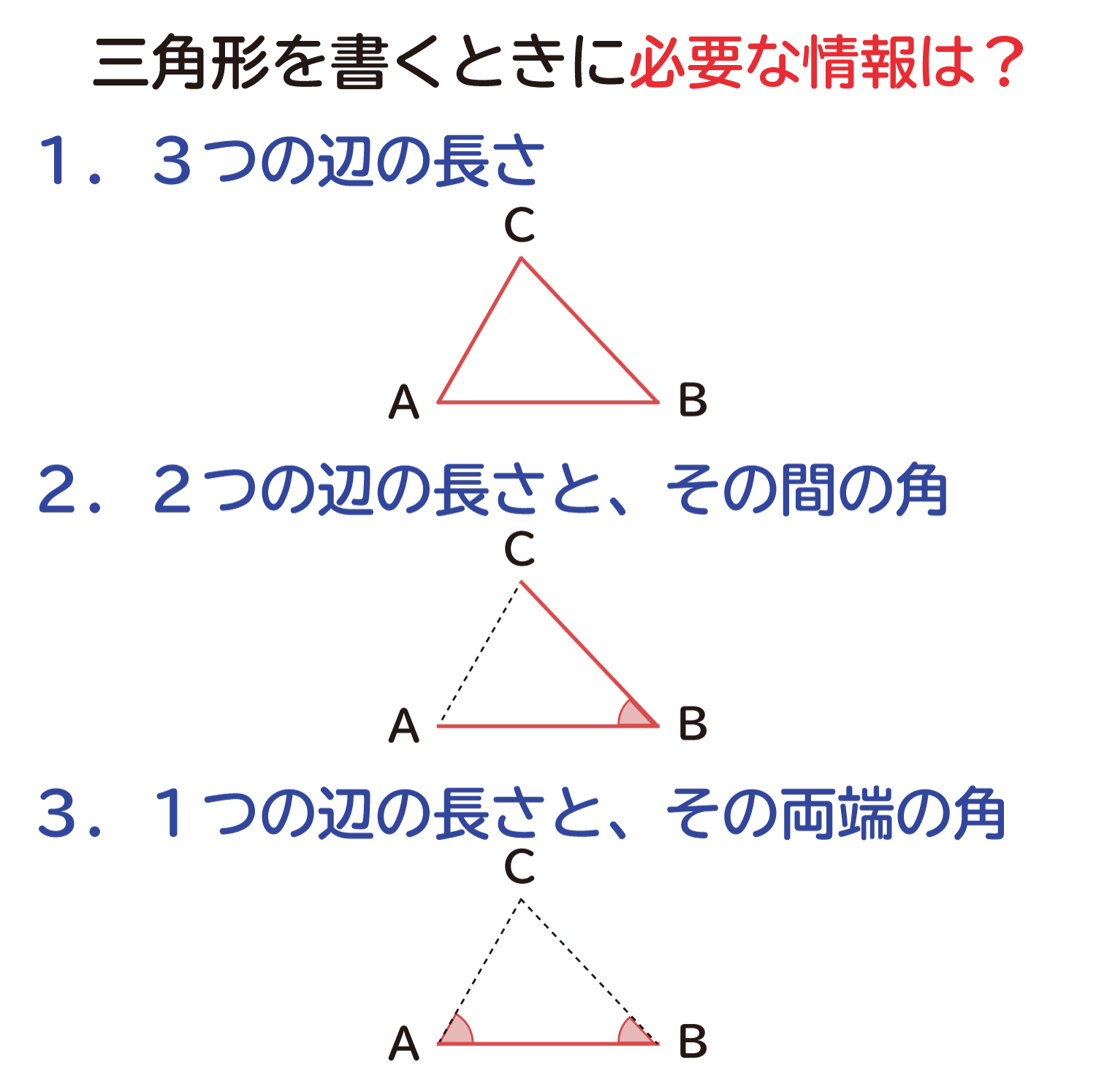



三角形の合同条件の説明 おかわりドリル
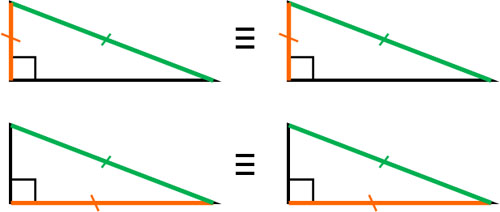



二等辺三角形 直角三角形の定義 合同条件と証明問題 Hatsudy 数学 科学




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院
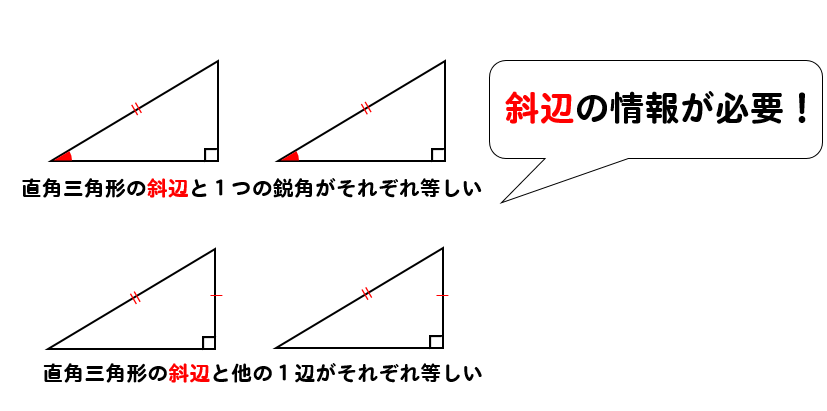



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材
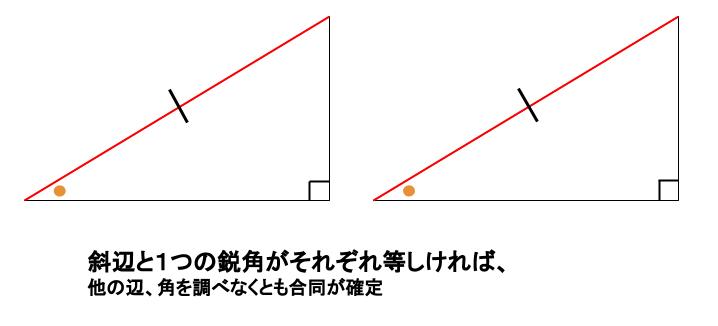



中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su
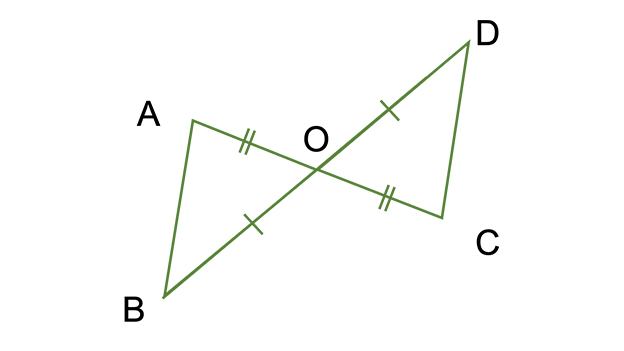



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
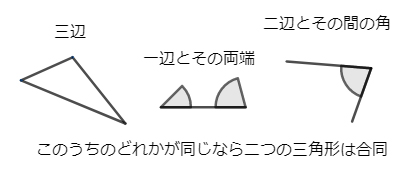



数学のアレ 何に役立つ 三角形の合同条件 同じ形の三角形を見つけて テストで5点くらいもらう 以外の使い方 1 2 ページ ねとらぼ




直角三角形の合同条件とその証明 数学fun



合同な三角形の組と合同条件 根拠含めて を教えて下さい Yahoo 知恵袋



中2数学 合同 三角形の合同条件まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



3




三角形の合同条件 Youtube
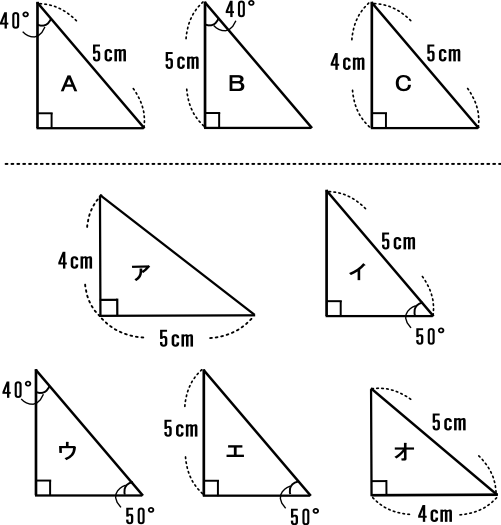



中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同
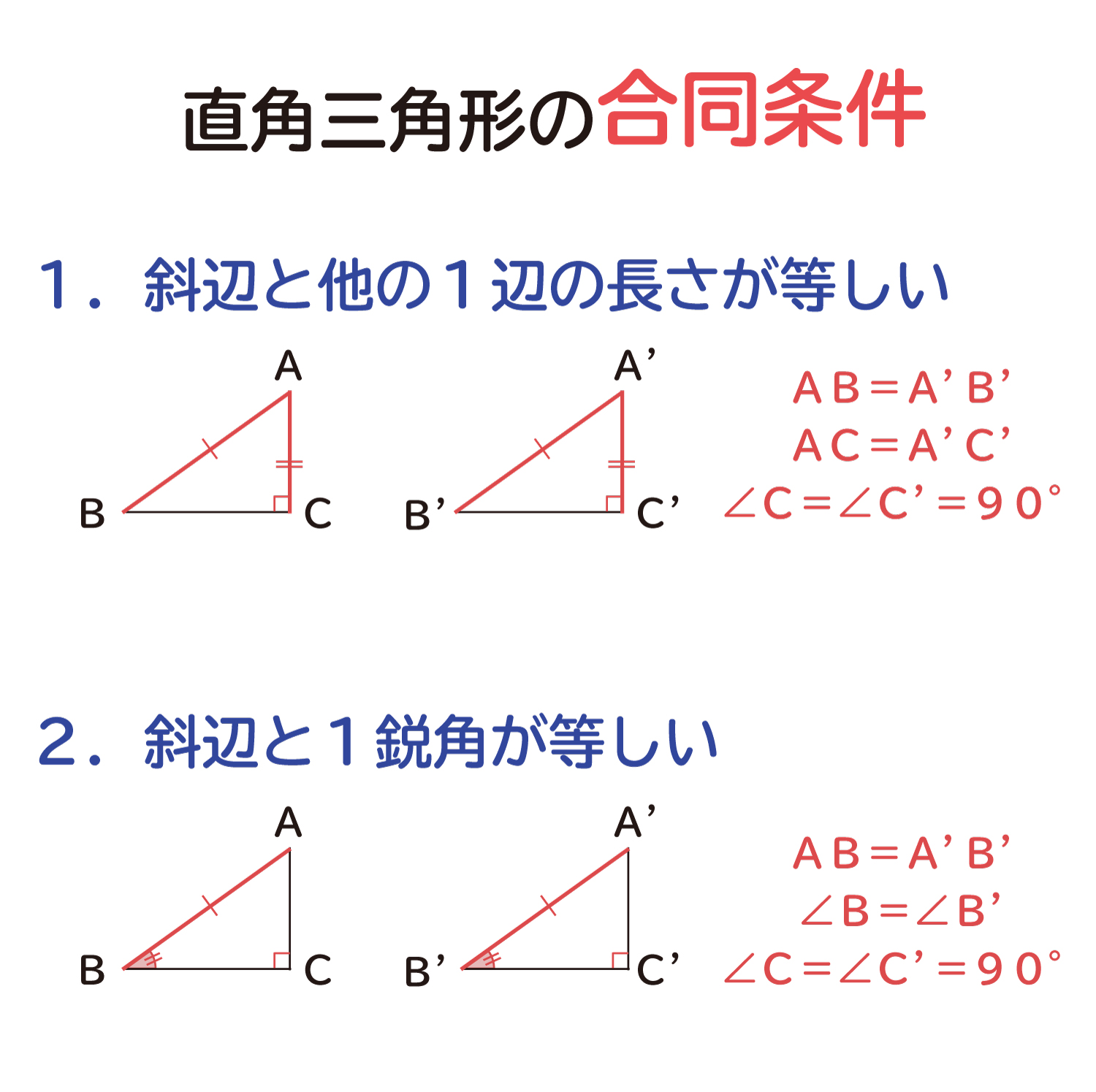



直角三角形の合同条件の説明 おかわりドリル




5分でわかる 三角形の3つの合同条件 Qikeru 学びを楽しくわかりやすく
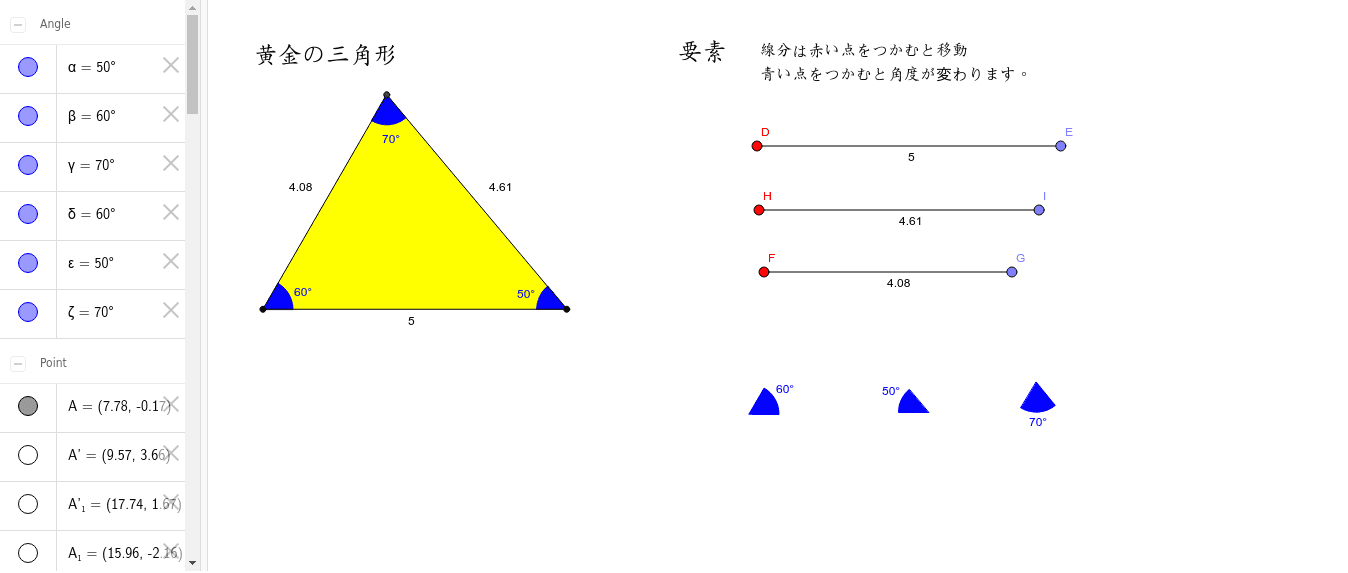



三角形の合同条件を見つける Geogebra




合同条件と性質について 中2 中3 家庭教師とっしゅ先生の授業 小学生 中学生
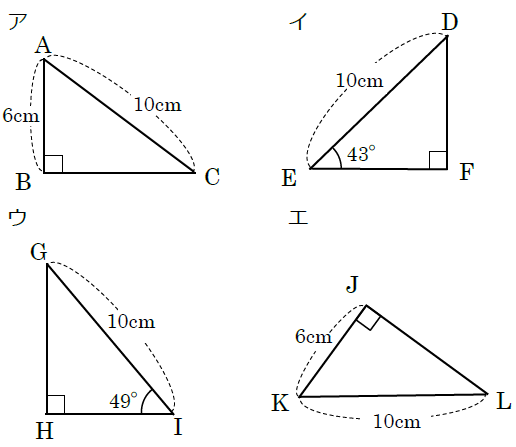



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン By 東京個別指導学院



0 件のコメント:
コメントを投稿